
| A、1 | B、2 | C、3 | D、4 |
| 1 |
| 2 |
| 5 |
| 2 |


科目:高中数学 来源: 题型:
| 1 |
| bnbn+1 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 2 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 2 |
| Sn |
| 2n+1 |
| 1 |
| 18 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| A、1个 | B、2个 | C、3个 | D、4个 |
查看答案和解析>>
科目:高中数学 来源: 题型:
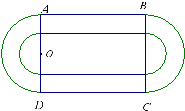 双峰一中是蔡和森的母校,已有百多年历史,学校教育教学质量稳步提高,今年高考喜获丰收,明年高考定会再创辉煌.为了贯彻全面发展的教育方针,学校决定新建造一个面积为10000平方米的运动场.如图,运动场是由一个矩形ABCD和分别以AD、BC为直径的两个半圆组成.跑道是一条宽8米的塑胶跑道,运动场除跑道外,其他地方均铺设草皮.已知塑胶跑道每平方米造价为150元,草皮每平方米造价为30元.
双峰一中是蔡和森的母校,已有百多年历史,学校教育教学质量稳步提高,今年高考喜获丰收,明年高考定会再创辉煌.为了贯彻全面发展的教育方针,学校决定新建造一个面积为10000平方米的运动场.如图,运动场是由一个矩形ABCD和分别以AD、BC为直径的两个半圆组成.跑道是一条宽8米的塑胶跑道,运动场除跑道外,其他地方均铺设草皮.已知塑胶跑道每平方米造价为150元,草皮每平方米造价为30元.查看答案和解析>>
科目:高中数学 来源: 题型:
| x2 |
| m-1 |
| y2 |
| 3-m |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com