
分析 分别设两个互相独立的飞机为x,y,根据题意表示出x与y的范围,由这两架飞机进入机场的时间之差不小于2分钟,飞机不会受到干扰,列出飞机受到干扰的事件发生x与y的关系式,找出约束条件$\left\{\begin{array}{l}{0≤x≤6}\\{0≤y≤6}\\{|x-y|≤2}\end{array}\right.$ 的可行域为如图阴影部分,阴影区域面积和正方形面积比值即为干扰发生的概率.
解答 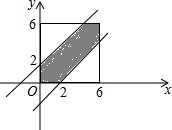 解:分别设两个互相独立的飞机为x,y,
解:分别设两个互相独立的飞机为x,y,
则所有事件集可表示为0≤x≤6,0≤y≤6,
由题目得,如果飞机受到干扰的事件发生,必有|x-y|≤2,
此时x,y满足$\left\{\begin{array}{l}{0≤x≤6}\\{0≤y≤6}\\{|x-y|≤2}\end{array}\right.$,约束条件$\left\{\begin{array}{l}{0≤x≤6}\\{0≤y≤6}\\{|x-y|≤2}\end{array}\right.$ 的可行域为如图阴影部分,
而所有事件的集合即为正方型面积,阴影区域面积为62-2×$\frac{1}{2}$×(6-2)2=36-16=20,
则阴影区域面积和正方形面积比值即为干扰发生的概率,即P=$\frac{20}{36}$=$\frac{5}{9}$,
故答案为:$\frac{5}{9}$.
点评 此题考查了几何概型,确定出约束条件的可行域是解本题的关键.


 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案科目:高中数学 来源: 题型:解答题
| 岁数x | 1 | 2 | 6 | 12 | 16 | 17 |
| 花费累积y(万元) | 1 | 2.8 | 9 | 17 | 22 | 24 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
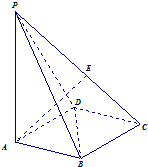 如图,底面为菱形的四棱锥P-ABCD中,PA⊥面ABCD,∠ABD=60°,E为PC上一动点,PA=AC.
如图,底面为菱形的四棱锥P-ABCD中,PA⊥面ABCD,∠ABD=60°,E为PC上一动点,PA=AC.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 在某海滨小城打的士收费办法如下:不超过3公里收8元,超过3公里的里程每公里收2.6元,另每车次超过3公里收燃油附加费1元(其他因素不考虑).相应x>3收费系统的流程图如图所示,则①处应填( )
在某海滨小城打的士收费办法如下:不超过3公里收8元,超过3公里的里程每公里收2.6元,另每车次超过3公里收燃油附加费1元(其他因素不考虑).相应x>3收费系统的流程图如图所示,则①处应填( )| A. | y=8+2.6x | B. | y=9+2.6x | C. | y=8+2.6(x-3) | D. | y=9+2.6(x-3) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 年级名次 是否近视 | 1~50 | 951~1000 |
| 近视 | 41 | 32 |
| 不近视 | 9 | 18 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 喜欢数学 | 不喜欢数学 | 总计 | |
| 男 | 37 | 85 | 122 |
| 女 | 35 | 143 | 178 |
| 总计 | 72 | 228 | 300 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com