
| 岁数x | 1 | 2 | 6 | 12 | 16 | 17 |
| 花费累积y(万元) | 1 | 2.8 | 9 | 17 | 22 | 24 |
分析 (1)利用公式计算$\overline{x}$,$\overline{y}$及系数a,b,可得回归方程;
(2)把x=24代入回归方程可得y值,即为预测父母为我们总的花费,然后除以240可得答案.
解答 解:(1)由题中表格数据得:$\overline{x}$=9,$\overline{y}$≈12.633,
$\sum_{i=1}^6{x_i}{y_i}$=1024.6,$\sum_{i=1}^6{{x_i}^2}$=730,
∴$\widehat{b}$=$\frac{\sum _{i=1}^{6}{x}_{i}{y}_{i}-6\overline{x}•\overline{y}}{\sum _{i=1}^{6}{{x}_{i}}^{2}-6{\overline{x}}^{2}}$=$\frac{1024-6×9×12.633}{730-6×9×9}$≈1.404,
$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$=12.633-1.404×9≈0.004,
故花费累积y与岁数x的线性回归直线方程为$\widehat{y}$=1.404 x+0.004;
(2)当x=24时,$\widehat{y}$=1.404×24+0.004=33.7(万元)
337000÷240≈1404(元)
所以每月要偿还1404元
点评 本题主要考查了线性回归分析的方法,包括散点图,用最小二乘法求参数,以及用回归方程进行预测等知识,考查了考生数据处理和运算能力.


科目:高中数学 来源: 题型:选择题
| 月份x | 1 | 2 | 3 | 4 |
| 用电量y | 45 | 40 | 30 | 25 |
| A. | 105 | B. | 51.5 | C. | 52 | D. | 52.5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | 2$\sqrt{3}$或$\sqrt{2}$ | C. | 2$\sqrt{3}$或$\sqrt{3}$ | D. | 2$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| $\overline{x}$ | $\overline{y}$ | $\overline{w}$ | $\sum_{i=1}^{8}({x}_{i}-\overline{x})^{2}$ | $\sum_{i=1}^{8}({w}_{i}-\overline{w})^{2}$ | $\sum_{i=1}^{8}({x}_{i}-\overline{x})({y}_{i}-\overline{y})$ | $\sum_{i=1}^{8}({w}_{i}-\overline{w})({y}_{i}-\overline{y)}$ |
| 46.6 | 563 | 6.8 | 289.8 | 1.6 | 1469 | 108.8 |

查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
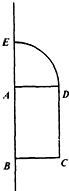 如图所示,矩形ABCD和一个圆心角为90°的扇形拼在一起,其中AB=2,BC=AE=1,则以AB所在直线为旋转轴将整个图形旋转一周所得几何体的表面积为( )
如图所示,矩形ABCD和一个圆心角为90°的扇形拼在一起,其中AB=2,BC=AE=1,则以AB所在直线为旋转轴将整个图形旋转一周所得几何体的表面积为( )| A. | 7π | B. | 5π | C. | 9π | D. | 8π |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com