
分析 设事件A在每次试验中发生的概率都是P,根据事件A至少发生一次的概率为$\frac{26}{27}$,求出p,再求出事件A恰好发生一次的概率.
解答 解:设事件A在每次试验中发生的概率都是P,则由事件A至少发生一次的概率为$\frac{26}{27}$,
可得 1-C30•P0•(1-P)3=$\frac{26}{27}$,
解得P=$\frac{2}{3}$.
故事件A恰好发生一次的概率为 C31•P•(1-P)2=3×$\frac{2}{3}$×($\frac{1}{3}$)2=$\frac{2}{9}$,
故答案为:$\frac{2}{9}$
点评 本题主要考查n次独立重复实验中恰好发生k次的概率,等可能事件的概率,所求的事件的概率等于用1减去它的对立事件概率,属于中档题


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | $2\sqrt{2}$ | C. | $\sqrt{5}$ | D. | $\sqrt{10}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 岁数x | 1 | 2 | 6 | 12 | 16 | 17 |
| 花费累积y(万元) | 1 | 2.8 | 9 | 17 | 22 | 24 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\left.\begin{array}{l}{a∥b}\\{b⊥α}\end{array}\right\}$⇒a⊥α | B. | $\left.\begin{array}{l}{a∥b}\\{b?α}\end{array}\right\}$⇒a∥α | C. | $\left.\begin{array}{l}{a⊥b}\\{b∥α}\end{array}\right\}$⇒a⊥α | D. | $\left.\begin{array}{l}{a⊥α}\\{a⊥b}\end{array}\right\}$⇒b?α |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
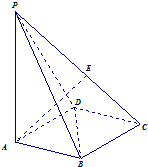 如图,底面为菱形的四棱锥P-ABCD中,PA⊥面ABCD,∠ABD=60°,E为PC上一动点,PA=AC.
如图,底面为菱形的四棱锥P-ABCD中,PA⊥面ABCD,∠ABD=60°,E为PC上一动点,PA=AC.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 年级名次 是否近视 | 1~50 | 951~1000 |
| 近视 | 41 | 32 |
| 不近视 | 9 | 18 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com