
分析 (Ⅰ)若f(x)-2=0在(0,3]上有两个不等实根,即x2+ax+1=0在(0,3]上有两个不等实根,令v(x)=x2+ax+1,则g(x)在(0,3]上有两个不等的零点,根据二次函数的图象和性质,构造关于a的不等式组,解得a的取值范围.
(Ⅱ)将问题转化为(f(x))max≥g(x),对$x∈[\frac{1}{2},1]$恒成立.对a进行分类讨论,最后综合讨论结果,可得答案.
解答 解:(Ⅰ)若f(x)-2=0在(0,3]上有两个不等实根,
即x2+ax+1=0在(0,3]上有两个不等实根,
令v(x)=x2+ax+1,则v(x)在(0,3]上有两个不等的零点,
则$\left\{\begin{array}{l}v(-\frac{a}{2})=\frac{4-{a}^{2}}{4}<0\\ v(3)=3a+10≥0\\ 0<-\frac{a}{2}<3\end{array}\right.$,
解得:$-\frac{10}{3}≤a<-2$…3分;
(Ⅱ)由题意,问题转化为(f(x))max≥g(x),对$x∈[\frac{1}{2},1]$恒成立.
对函数$g(x)=\frac{{a{x^2}+x+a}}{x^2}$,令$\frac{1}{x}=t∈[1,2]$,
$g(x)=\frac{{a{x^2}+x+a}}{x^2}=h(t)=a{t^2}+t+a$,
则问题转化为:(f(x))max≥h(t),t∈[1,2]恒成立.
∵${(f(x))_{max}}=\left\{\begin{array}{l}-2a-3,a≤-4\\ \frac{a^2}{4}+1,-4<a<-2\\-a,a≥-2\end{array}\right.$,…(5分)
(1)当a≤-4时,-2a-3≥at2+t+a对t∈[1,2]恒成立,
则$a≤-\frac{t+3}{{{t^2}+2}}$对t∈[1,2]恒成立,
得$a≤-\frac{4}{3}$,得a≤-4;…(6分)
(2)当-4<a<-2时,$\frac{a^2}{4}+1≥a{t^2}+t+a$对t∈[1,2]恒成立,
则$H(t)=a{t^2}+t+a-1-\frac{a^2}{4}≤0$对t∈[1,2]恒成立,
关于t的二次函数的对称轴在$[-\frac{1}{4},-\frac{1}{8}]$之间,开口向下,
则H(1)≤0,
得a≤0,a≥8,即得-4<a<-2;…(7分)
(3)当a≥-2时,-a≥at2+t+a对t∈[1,2]恒成立,
则$a≤\frac{-t}{{{t^2}+2}}$对t∈[1,2]恒成立,
得$a≤-\frac{{\sqrt{2}}}{4}$,得$-2≤a≤-\frac{{\sqrt{2}}}{4}$;…(8分)
综上,得满足题意的a的范围是:$a≤-\frac{{\sqrt{2}}}{4}$.…(9分)
点评 本题考查的知识点是二次函数的图象和性质,恒成立问题,函数的最值,分类讨论思路,分段函数的应用,综合性强,分类复杂,运算强度较大,属于难题.


科目:高中数学 来源: 题型:选择题
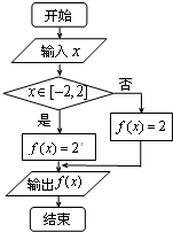 阅读程序框图,如果输出的函数值在区间[2,4]内,则输入的实数x的取值范围是( )
阅读程序框图,如果输出的函数值在区间[2,4]内,则输入的实数x的取值范围是( )| A. | (-∞,-2] | B. | (-∞,-2) | C. | [1,+∞) | D. | (-∞,-2)∪[1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 关于x轴对称 | B. | 关于y轴对称 | ||
| C. | 关于直线x-y=0对称 | D. | 关于直线x+y=0对称 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 月份x | 1 | 2 | 3 | 4 |
| 用电量y | 45 | 40 | 30 | 25 |
| A. | 105 | B. | 51.5 | C. | 52 | D. | 52.5 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com