
分析 设出椭圆上的点P(x0,y0),利用焦半径公式,表示出|PO|2=|PF1|•|PF2|,求出点的坐标,得出结论.
解答 解:设椭圆上的点P(x0,y0),则$\frac{{x}_{0}^{2}}{{a}^{2}}+\frac{{y}_{0}^{2}}{{b}^{2}}=1$,y02=b2(1-$\frac{{x}_{0}^{2}}{{a}^{2}}$),
椭圆的第二定义可知:|PF1|=a-ex0,|PF2|=a+ex0,
因为|PO|2=|PF1|•|PF2|,则x02+y02=a2-e2x02,
则有x02+b2(1-$\frac{{x}_{0}^{2}}{{a}^{2}}$)=x02+y02,解得x0=±$\frac{\sqrt{2}a}{2}$,
因此满足条件的有四个点,
故答案为:4.
点评 本题考查了椭圆的新定义问题,解题时应利用焦半径列出方程,求出点的坐标,是基础题.


 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案科目:高中数学 来源: 题型:选择题
| A. | A∩B=∅ | B. | ∁UA∪B=R | C. | A∩B=B | D. | A∪B=B |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{4}$ | B. | $\frac{{\sqrt{3}π}}{4}$ | C. | $\frac{π}{8}$ | D. | $\frac{{\sqrt{3}π}}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
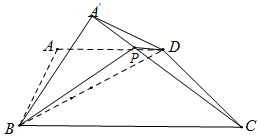 如图,已知等腰梯形ABCD中,AD∥BC,BC=2AD=2AB=4,将△ABC沿BD折到△A′BD的位置,使平面A′BD⊥平面CBD.
如图,已知等腰梯形ABCD中,AD∥BC,BC=2AD=2AB=4,将△ABC沿BD折到△A′BD的位置,使平面A′BD⊥平面CBD.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com