
| A. | y=$\sqrt{x}$ | B. | y=|sinx| | C. | y=ex-e-x | D. | y=cosx |
分析 根据题意,依次分析选项中函数的奇偶性,综合即可得答案.
解答 解:根据题意,依次分析选项:
对于A、y=$\sqrt{x}$,其定义域为{x|x≥0},不关于原点对称,不是奇函数,不符合题意;
对于B、y=|sinx|,其定义域为R,f(-x)=|sin(-x)|=sinx|=f(x),为偶函数,不符合题意;
对于C、y=ex-e-x,其定义域为R,f(-x)=e-x-ex=-(ex-e-x)=-f(-x),为奇函数,符合题意;
对于D、y=cosx,其定义域为R,f(-x)=cos(-x)=cosx=f(x),为偶函数,不符合题意;
故选:C.
点评 本题考查函数奇偶性的判定,注意先分析函数定义域.


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:高中数学 来源: 题型:解答题
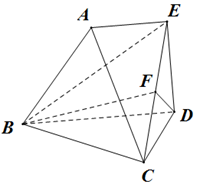 如图所示,在多面体ABCDE中,△BCD是边长为2的正三角形,AE∥DB,AE⊥DE,2AE=BD,DE=1,面ABDE⊥面BCD,F是CE的中点.
如图所示,在多面体ABCDE中,△BCD是边长为2的正三角形,AE∥DB,AE⊥DE,2AE=BD,DE=1,面ABDE⊥面BCD,F是CE的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=±$\frac{\sqrt{2}}{2}$x | B. | y=±$\frac{\sqrt{3}}{3}$x | C. | y=±$\frac{1}{2}$x | D. | y=±$\frac{1}{3}$x |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
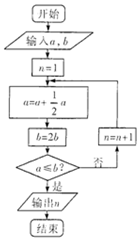 数学名著《算学启蒙》中有如下问题:“松长五尺,竹长两尺,松日自半,竹日自倍,松竹何日而长等.”如图是源于其思想的一个程序框图,若输入的a,b的值分别为16,4,则输出的n的值为( )
数学名著《算学启蒙》中有如下问题:“松长五尺,竹长两尺,松日自半,竹日自倍,松竹何日而长等.”如图是源于其思想的一个程序框图,若输入的a,b的值分别为16,4,则输出的n的值为( )| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com