
分析 (1)由题意,可得f(1)=0,即可求得a的大小;
(2)要证存在唯一的x0∈(x1,x2),使直线AB的斜率等于f′(x0),只需证明存在点Q(x0,f(x0)),x1<x0<x2,使得f′(x0)=k${\;}_{{x}_{1}{x}_{2}}$.由f′(x)=$\frac{1}{x}$-a,即证存在x0∈(x1,x2),使得 $\frac{1}{{x}_{0}}$-a=$\frac{ln{x}_{2}-a{x}_{2}-ln{x}_{1}+a{x}_{1}}{{x}_{2}-{x}_{1}}$,即x0lnx2-x0lnx1+x1-x2=0成立,即方程xlnx2-xlnx1+x1-x2=0在(x1,x2)内有解.设F(x)=xlnx2-xlnx1+x1-x2,0<x<x2.由零点存在定理和函数的单调性,即可得证.
解答 (1))解:由题意,f(1)=0,得,$ln\frac{1}{a}$=0,所以a=1,…(2分)
(2)证明:h(x)=lnx-ex.∵h'(x0)=k AB,∴$\frac{1}{x_0}-e=\frac{{ln{x_2}-ln{x_1}-e({{x_2}-{x_1}})}}{{{x_2}-{x_1}}}$,
∴$\frac{{{x_2}-{x_1}}}{x_0}-ln\frac{x_2}{x_1}=0$,即${x_0}ln\frac{x_2}{x_1}-({{x_2}-{x_1}})=0$,…(6分)
设$φ(x)=xln\frac{x_2}{x_1}-({{x_2}-{x_1}})$,则φ(x)是关于x的一次函数,
故要在区间(x1,x2)证明存在唯一性,只需证明φ(x)在(x1,x2)上满足φ(x1)•φ(x2)<0.
下面证明之:$φ({x_1})={x_1}ln\frac{x_2}{x_1}-({{x_2}-{x_1}})$,$φ({x_2})={x_2}ln\frac{x_2}{x_1}-({{x_2}-{x_1}})$,
为了判断φ(x1),φ(x2)的符号,可以分别将x1,x2看作自变量得到两个新函数φ(x1),φ(x2),
讨论他们的最值:$φ({x_1})={x_1}ln\frac{x_2}{x_1}-({{x_2}-{x_1}})$,将x1看作自变量求导得$φ'({x_1})=ln\frac{x_2}{x_1}>0$,
∴φ(x1)是x1的增函数,∵x1<x2,∴$φ({x_1})<φ({x_2})={x_2}ln\frac{x_2}{x_2}-({{x_2}-{x_2}})=0$;
同理:$φ({x_2})={x_2}ln\frac{x_2}{x_1}-({{x_2}-{x_1}})$,将x2看作自变量求导得$φ'({x_2})=ln\frac{x_2}{x_1}>0$,
∴φ(x2)是x2的增函数,∵x1<x2,∴$φ({x_2})<φ({x_1})={x_1}ln\frac{x_1}{x_1}-({{x_1}-{x_1}})=0$;
∴φ(x1)•φ(x2)<0,∴函数$φ(x)=xln\frac{x_2}{x_1}-({{x_2}-{x_1}})$在(x1,x2)内有零点x0…(10分)
又$\frac{x_2}{x_1}>1$,∴$ln\frac{x_2}{x_1}>0$,函数$φ(x)=xln\frac{x_2}{x_1}-({{x_2}-{x_1}})$在(x1,x2)是增函数,
∴函数$φ(x)=xln\frac{x_2}{x_1}-({{x_2}-{x_1}})$在(x1,x2)内有唯一零点x0,从而命题成立.…(12分)
点评 本题考查导数的综合运用:导数的几何意义,同时考查函数的零点存在定理和函数方程的思想,运用构造函数和单调性是解题的关键.


 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{2}$ | B. | π | C. | 2π | D. | 4π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 参与调查问卷次数 | [0,2) | [2,4) | [4,6) | [6,8) | [8,10) | [10,12] |
| 参与调查问卷人数 | 8 | 14 | 8 | 14 | 10 | 6 |
| 男 | 女 | 合计 | |
| 积极上网参政议政 | 8 | ||
| 不积极上网参政议政 | |||
| 合计 | 40 |
| P(k2>k0) | 0.100 | 0.050 | 0.010 |
| k0 | 2.706 | 3.841 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,$\frac{1}{e}}$) | B. | ($\frac{1}{e}$,e) | C. | (e,+∞) | D. | (0,$\frac{1}{e}}$)∪(e,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(sin α)>f(cos β) | B. | f(cos α)<f(cos β) | C. | f(cos α)>f(sin β) | D. | f(sin α)<f(sin β) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
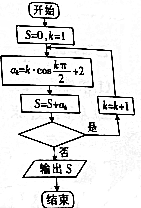
| A. | k<2015? | B. | k<2016? | C. | k<2017? | D. | k<2018? |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
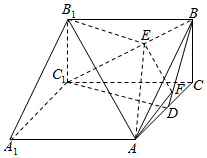 如图,三棱柱ABC-A1B1C1中,BC垂直于正方形A1ACC1所在平面,AC=2,BC=1,D为AC中点,E为线段BC1上的一点(端点除外),平面AB1E与BD交于点F
如图,三棱柱ABC-A1B1C1中,BC垂直于正方形A1ACC1所在平面,AC=2,BC=1,D为AC中点,E为线段BC1上的一点(端点除外),平面AB1E与BD交于点F查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com