
| A. | $\frac{π}{2}$ | B. | π | C. | 2π | D. | 4π |
分析 利用折成直二面角推出AB⊥BC,CD⊥AD.取AC的中点O,说明外接球的球心是O,求出外接球的半径,然后求解表面积.
解答 解:如图,因为平面BDC⊥平面ABD(折成直二面角),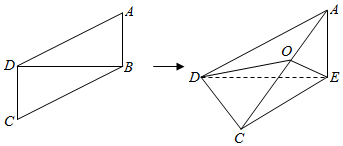
所以AB⊥平面BDC,CD⊥平面ABD,得AB⊥BC,CD⊥AD.
取AC的中点O,则OA=OB=OC=OD.
于是外接球的球心是O,OA=$\frac{1}{2}$AC.
而AC2=AB2+BC2=$\frac{1}{2}$(4AB2+2BD2)=$\frac{1}{2}$.
所以半径OA=$\frac{\sqrt{2}}{4}$.
于是外接球的表面积为S=4π•OA2=$\frac{π}{2}$.
故选:A.
点评 本题考查几何体的外接球的表面积的求法,判断外接球的球心是解题的关键,考查计算能力.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | 2,14,26,38,42,56 | B. | 5,8,31,36,48,54 | ||
| C. | 3,13,23,33,43,53 | D. | 5,10,15,20,25,30 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
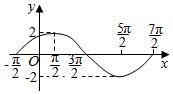 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π,x∈R)在一个周期内的图象如图所示,则函数的解析式为f(x)=2sin($\frac{1}{2}$x+$\frac{π}{4}$)..直线y=$\sqrt{3}$与函数y=f(x)(x∈R)图象的所有交点的坐标为($\frac{π}{6}$+4kπ,$\sqrt{3}$)或($\frac{5π}{6}$+4kπ,$\sqrt{3}$)(k∈Z).
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π,x∈R)在一个周期内的图象如图所示,则函数的解析式为f(x)=2sin($\frac{1}{2}$x+$\frac{π}{4}$)..直线y=$\sqrt{3}$与函数y=f(x)(x∈R)图象的所有交点的坐标为($\frac{π}{6}$+4kπ,$\sqrt{3}$)或($\frac{5π}{6}$+4kπ,$\sqrt{3}$)(k∈Z).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
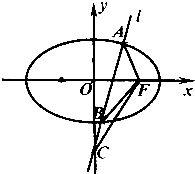 如图,椭圆x2+2y2=1的右焦点为F,直线l不经过焦点,与椭圆相交于点A,B,与y轴的交点为C,则△BCF与△ACF的面积之比是( )
如图,椭圆x2+2y2=1的右焦点为F,直线l不经过焦点,与椭圆相交于点A,B,与y轴的交点为C,则△BCF与△ACF的面积之比是( )| A. | |$\frac{|BF|-1}{|AF|-1}$| | B. | |$\frac{|BF{|}^{2}-1}{|AF{|}^{2}-1}$| | C. | $\frac{|BF|+1}{|AF|+1}$ | D. | $\frac{|BF{|}^{2}+1}{|AF{|}^{2}+1}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p1<p2<p3 | B. | p2<p3<p1 | C. | p1<p3<p2 | D. | p3<p2<p1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com