
| A. | p1<p2<p3 | B. | p2<p3<p1 | C. | p1<p3<p2 | D. | p3<p2<p1 |
分析 作出每个事件对应的平面区域,求出对应的面积,利用几何概型的概率公式进行计算比较即可.
解答 解:分别作出事件对应的图象如图1、2、3(阴影部分)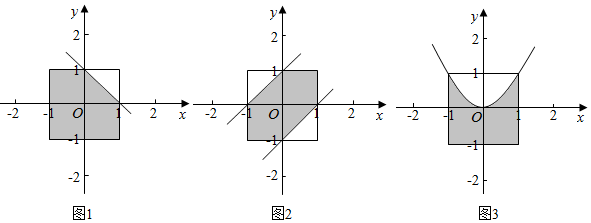
则阴影部分的面积S1=4-$\frac{1}{2}×1×1$=$\frac{7}{2}$,S2=4-$\frac{1}{2}×1×1$×2=3,
S3=${∫}_{-1}^{1}({x}^{2}+1)dx$=($\frac{1}{3}{x}^{3}+x$)${|}_{-1}^{1}$=$\frac{8}{3}$,
∴S3<S2<S1,
即P3<P2<P1,
故选:D.
点评 本题主要考查几何概型的概率计算,利用数形结合是解决本题的关键.本题也可以直接通过图象比较面积的大小即可比较大小.


 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{2}$ | B. | π | C. | 2π | D. | 4π |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 参与调查问卷次数 | [0,2) | [2,4) | [4,6) | [6,8) | [8,10) | [10,12] |
| 参与调查问卷人数 | 8 | 14 | 8 | 14 | 10 | 6 |
| 男 | 女 | 合计 | |
| 积极上网参政议政 | 8 | ||
| 不积极上网参政议政 | |||
| 合计 | 40 |
| P(k2>k0) | 0.100 | 0.050 | 0.010 |
| k0 | 2.706 | 3.841 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,$\frac{1}{e}}$) | B. | ($\frac{1}{e}$,e) | C. | (e,+∞) | D. | (0,$\frac{1}{e}}$)∪(e,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
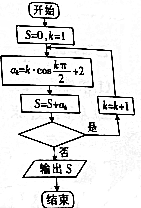
| A. | k<2015? | B. | k<2016? | C. | k<2017? | D. | k<2018? |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com