
如图,在直四棱柱 中,底面ABCD为等腰梯形,AB∥CD,AB="4,BC=CD=2," AA
中,底面ABCD为等腰梯形,AB∥CD,AB="4,BC=CD=2," AA ="2, " E、E
="2, " E、E 、F分别是棱AD、AA
、F分别是棱AD、AA 、AB的中点。
、AB的中点。
(Ⅰ)证明:直线 ∥平面
∥平面 ;w.w.w.k.s.5.u.c.o.m
;w.w.w.k.s.5.u.c.o.m 

(Ⅱ)求二面角 的余弦值
的余弦值
(Ⅱ)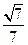
解析解法一:(1)在直四棱柱ABCD-A B
B C
C D
D 中,取A1B1的中点F1,
中,取A1B1的中点F1,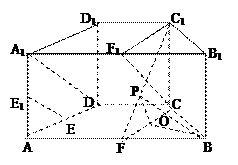 连接A1D,C1F1,CF1,因为AB="4," CD=2,且AB//CD,
连接A1D,C1F1,CF1,因为AB="4," CD=2,且AB//CD,
所以CDA1F1,A1F1CD为平行四边形,所以CF1//A1D,
又因为E、E 分别是棱AD、AA
分别是棱AD、AA 的中点,所以EE1//A1D,
的中点,所以EE1//A1D,
所以CF1//EE1,又因为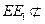 平面FCC
平面FCC ,
,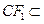 平面FCC
平面FCC ,
,
所以直线EE //平面FCC
//平面FCC .······6分
.······6分
(2)因为AB="4," BC="CD=2," 、F是棱AB的中点,所以BF=BC=CF,△BCF为正三角形,取CF的中点O,则OB⊥CF,又因为直四棱柱ABCD-A B
B C
C D
D 中,CC1⊥平面ABCD,所以CC1⊥BO,所以OB⊥平面CC1F,过O在平面CC1F内作OP⊥C1F,垂足为P,连接BP,则∠OPB为二面角B-FC
中,CC1⊥平面ABCD,所以CC1⊥BO,所以OB⊥平面CC1F,过O在平面CC1F内作OP⊥C1F,垂足为P,连接BP,则∠OPB为二面角B-FC -C的一个平面角, 在△BCF为正三角形中,
-C的一个平面角, 在△BCF为正三角形中,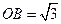 ,在Rt△CC1F中, △OPF∽△CC1F,∵
,在Rt△CC1F中, △OPF∽△CC1F,∵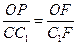 ∴
∴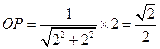 , w.w.w.k.s.5.u.c.o.m
, w.w.w.k.s.5.u.c.o.m 
 ··········11分
··········11分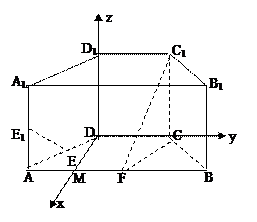
在Rt△OPF中,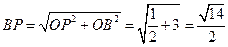 ,
,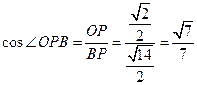 ,所以
,所以
二面角B-FC -C的余弦值为
-C的余弦值为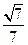 .·······14分
.·······14分


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
(本小题满分14分)
已知四棱锥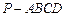 ,底面
,底面 为矩形,侧棱
为矩形,侧棱 ,其中
,其中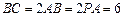 ,
,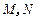 为侧棱
为侧棱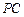 上的两个三等分点,如图所示.
上的两个三等分点,如图所示.
(Ⅰ)求证: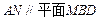 ;
;
(Ⅱ)求异面直线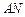 与
与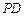 所成角的余弦值;
所成角的余弦值;
(Ⅲ)求二面角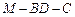 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
如图,在三棱锥S﹣ABC中,底面是边长为1的等边三角形,侧棱长均为2,SO⊥底面ABC,O为垂足,则侧棱SA与底面ABC所成角的余弦值为( )
A. | B. | C. | D. |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分12分)
右图为一简单组合体,其底面ABCD为正方形, 平面
平面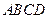 ,
,  ,且
,且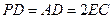 ="2" .
="2" .
(1)答题卡指定的方框内画出该几何体的三视图;
(2)求四棱锥B-CEPD的体积. 

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(12分)如图,在三棱锥P—ABC中,PA⊥底面ABC,∠BAC=60°,AB=AC=2 ,以PA为直径的球O和PB、PC分别交于B1、C1
,以PA为直径的球O和PB、PC分别交于B1、C1
(1)求证B1C1∥平面ABC
(2)若二面角C—PB—A的大小为arctan2 ,试求球O的表面积。
,试求球O的表面积。
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
已知m,n为两条不同的直线, 为两个不同的平面,
为两个不同的平面, ,则下列命题中的假命题是( )
,则下列命题中的假命题是( )
A.若m//n,则 |
B.若 ,则 ,则 |
C.若 相交,则 相交,则 相交 相交 |
D.若 相交,则 相交,则 相交 相交 |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
已知α,β是两个不同的平面,给出下列四个条件:
①存在一条直线a,a⊥α,a⊥β;
②存在一个平面γ,γ⊥α,γ⊥β;
③存在两条平行直线a,b,a?α,b?β,a∥β,b∥α;
④存在两条异面直线a,b,a?α,b?β,a∥β,b∥α.
可以推出α∥β的是( )
| A.①③ | B.②④ | C.①④ | D.②③ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com