
【题目】某高校在2016年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组,得到的频率分布表如下表所示.
组号 | 分组 | 频数 | 频率 |
第1组 |
| 5 | 0.050 |
第2组 |
| n | 0.350 |
第3组 |
| 30 | p |
第4组 |
| 20 | 0.200 |
第5组 |
| 10 | 0.100 |
合计 | 100 | 1.000 |
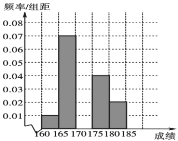
(1)求频率分布表中n,p
(2)为了能选拔出最优秀的学生,高校决定在笔试成绩高的第3、4、5组中用分层抽样的方法抽取6名学生进入第二轮面试,则第3、4、5组每组各抽取多少名学生进入第二轮面试?
(3)在(2)的前提下,学校决定从6名学生中随机抽取2名学生接受甲考官的面试,求第4组至少有1名学生被甲考官面试的概率.
【答案】(1)![]() ,
,![]() ,中位数估计值为171.7(2)第3、4、5组每组各抽学生人数为3、2、1(3)
,中位数估计值为171.7(2)第3、4、5组每组各抽学生人数为3、2、1(3)![]()
【解析】
(1)由频率分布表可得:![]() ,
,![]() ,由中位数的求法可得中位数估计值为171.7;
,由中位数的求法可得中位数估计值为171.7;
(2)因为笔试成绩高的第3、4、5组的人数之比为![]() ,由分层抽样的方法选6名学生,三个小组分别选的人数为3、2、1;
,由分层抽样的方法选6名学生,三个小组分别选的人数为3、2、1;
(3)先列举出从6名学生中随机抽取2名学生的不同取法,再列举出第4组至少有1名学生被甲考官面试的取法,再结合古典概型的概率公式即可得解.
解:(1)由已知:![]() ,
,
![]() ,
,
![]() ,
,![]() ,中位数为
,中位数为![]()
![]() 171.7,
171.7,
即中位数估计值为171.7,
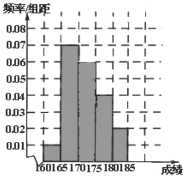
(2)由已知,笔试成绩高的第3、4、5组的人数之比为![]() ,现用分层抽样的方法选6名学生。故第3、4、5组每组各抽学生人数为3、2、1。
,现用分层抽样的方法选6名学生。故第3、4、5组每组各抽学生人数为3、2、1。
(3)在(2)的前提下,记第3组的3名学生为![]() ,
,![]() ,
,![]() ,
,
第4组的2名学生为![]() ,
,![]() ,第5组的1名学生为
,第5组的1名学生为![]() ,且“第4组至少有1名学生被甲考官面试”为事件A。
,且“第4组至少有1名学生被甲考官面试”为事件A。
则所有的基本事件有:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,一共15种。
,一共15种。
A事件有:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,一共9种。
,一共9种。
![]() ,
,
答:第4组至少有1名学生被甲考官面试的概率为![]() 。
。


科目:高中数学 来源: 题型:
【题目】下列说法错误的是( )
A.命题“若![]() ,则
,则![]() ”的逆否命题是“若
”的逆否命题是“若![]() ,则
,则![]() ”
”
B.“![]() ”是“
”是“![]() ”的充分不必要条件
”的充分不必要条件
C.若![]() 为假命题,则
为假命题,则![]() 、
、![]() 均为假命题
均为假命题
D.命题![]() :“
:“![]() ,使得
,使得![]() ”,则非
”,则非![]() :“
:“![]() ,
,![]() ”
”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,以原点O为极点,x轴的正半轴为极轴建立极坐标系,已知直线l的参数方程为: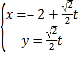 ,
,![]() 为参数
为参数![]() 点的极坐标为
点的极坐标为![]() ,曲线C的极坐标方程为
,曲线C的极坐标方程为![]() .
.
![]() Ⅰ
Ⅰ![]() 试将曲线C的极坐标方程化为直角坐标方程,并求曲线C的焦点在直角坐标系下的坐标;
试将曲线C的极坐标方程化为直角坐标方程,并求曲线C的焦点在直角坐标系下的坐标;
![]() Ⅱ
Ⅱ![]() 设直线l与曲线C相交于两点A,B,点M为AB的中点,求
设直线l与曲线C相交于两点A,B,点M为AB的中点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}为等比数列,a1=2,公比q>0,且a2,6,a3成等差数列.
(1)求数列{an}的通项公式;
(2)设bn=log2an,![]() ,求使
,求使![]() 的n的值.
的n的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在![]() 中,已知
中,已知![]() ,
,![]() ,
,![]() ,D是边AC上一点,将
,D是边AC上一点,将![]() 沿BD折起,得到三棱锥
沿BD折起,得到三棱锥![]() .若该三棱锥的顶点A在底面BCD的射影M在线段BC上,设
.若该三棱锥的顶点A在底面BCD的射影M在线段BC上,设![]() ,则x的取值范围为( )
,则x的取值范围为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为践行“绿水青山就是金山银山”的发展理念,某城区对辖区内![]() ,
,![]() ,
,![]() 三类行业共200个单位的生态环境治理成效进行了考核评估,考评分数达到80分及其以上的单位被称为“星级”环保单位,未达到80分的单位被称为“非星级”环保单位.现通过分层抽样的方法获得了这三类行业的20个单位,其考评分数如下:
三类行业共200个单位的生态环境治理成效进行了考核评估,考评分数达到80分及其以上的单位被称为“星级”环保单位,未达到80分的单位被称为“非星级”环保单位.现通过分层抽样的方法获得了这三类行业的20个单位,其考评分数如下:
![]() 类行业:85,82,77,78,83,87;
类行业:85,82,77,78,83,87;
![]() 类行业:76,67,80,85,79,81;
类行业:76,67,80,85,79,81;
![]() 类行业:87,89,76,86,75,84,90,82.
类行业:87,89,76,86,75,84,90,82.
(Ⅰ)计算该城区这三类行业中每类行业的单位个数;
(Ⅱ)若从抽取的![]() 类行业这6个单位中,再随机选取3个单位进行某项调查,求选出的这3个单位中既有“星级”环保单位,又有“非星级”环保单位的概率.
类行业这6个单位中,再随机选取3个单位进行某项调查,求选出的这3个单位中既有“星级”环保单位,又有“非星级”环保单位的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com