
【题目】为践行“绿水青山就是金山银山”的发展理念,某城区对辖区内![]() ,
,![]() ,
,![]() 三类行业共200个单位的生态环境治理成效进行了考核评估,考评分数达到80分及其以上的单位被称为“星级”环保单位,未达到80分的单位被称为“非星级”环保单位.现通过分层抽样的方法获得了这三类行业的20个单位,其考评分数如下:
三类行业共200个单位的生态环境治理成效进行了考核评估,考评分数达到80分及其以上的单位被称为“星级”环保单位,未达到80分的单位被称为“非星级”环保单位.现通过分层抽样的方法获得了这三类行业的20个单位,其考评分数如下:
![]() 类行业:85,82,77,78,83,87;
类行业:85,82,77,78,83,87;
![]() 类行业:76,67,80,85,79,81;
类行业:76,67,80,85,79,81;
![]() 类行业:87,89,76,86,75,84,90,82.
类行业:87,89,76,86,75,84,90,82.
(Ⅰ)计算该城区这三类行业中每类行业的单位个数;
(Ⅱ)若从抽取的![]() 类行业这6个单位中,再随机选取3个单位进行某项调查,求选出的这3个单位中既有“星级”环保单位,又有“非星级”环保单位的概率.
类行业这6个单位中,再随机选取3个单位进行某项调查,求选出的这3个单位中既有“星级”环保单位,又有“非星级”环保单位的概率.
【答案】(Ⅰ)![]() ,
,![]() ,
,![]() 三类行业中每类行业的单位个数分别为60,60,80.(Ⅱ)
三类行业中每类行业的单位个数分别为60,60,80.(Ⅱ)![]()
【解析】
第一问利用分层抽样的概念直接计算即可;第二问是古典概率模型,先列出所有的基本事件,然后再找出3个单位都是“星级”环保单位或都是“非星级”环保单位所包含基本事件的个数,即可求出3个单位中既有“星级”环保单位,又有“非星级”环保单位的概率。
(I)由题意,得抽取的![]() ,
,![]() ,
,![]() 三类行业单位个数之比为
三类行业单位个数之比为![]() .
.
由分层抽样的定义,有
![]() 类行业的单位个数为
类行业的单位个数为![]() ,
,
![]() 类行业的单位个数为
类行业的单位个数为![]() ,
,
![]() 类行业的单位个数为
类行业的单位个数为![]() ,
,
故该城区![]() ,
,![]() ,
,![]() 三类行业中每类行业的单位个数分别为60,60,80.
三类行业中每类行业的单位个数分别为60,60,80.
(Ⅱ)记选出的这3个单位中既有“星级”环保单位,又有“非星级”环保单位为事件![]() .
.
这3个单位的考核数据情形有![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,共20种.
,共20种.
这3个单位都是“星级”环保单位的考核数据情形有![]() ,
,![]() ,
,![]() ,
,![]() ,共4种,没有都是“非星级”环保单位的情形,
,共4种,没有都是“非星级”环保单位的情形,
故这3个单位都是“星级”环保单位或都是“非星级”环保单位的情形共4种,
故所求概率![]() .
.


科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的右焦点为
的右焦点为![]() ,离心率为
,离心率为![]() 。
。
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)![]() 是椭圆
是椭圆![]() 上不同的三点,若直线
上不同的三点,若直线![]() 的斜率之积为
的斜率之积为![]() ,试问从
,试问从![]() 两点的横坐标之和是否为定值?若是,求出这个定值;若不是,请说明理由。
两点的横坐标之和是否为定值?若是,求出这个定值;若不是,请说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高校在2016年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组,得到的频率分布表如下表所示.
组号 | 分组 | 频数 | 频率 |
第1组 |
| 5 | 0.050 |
第2组 |
| n | 0.350 |
第3组 |
| 30 | p |
第4组 |
| 20 | 0.200 |
第5组 |
| 10 | 0.100 |
合计 | 100 | 1.000 |
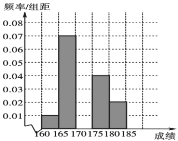
(1)求频率分布表中n,p
(2)为了能选拔出最优秀的学生,高校决定在笔试成绩高的第3、4、5组中用分层抽样的方法抽取6名学生进入第二轮面试,则第3、4、5组每组各抽取多少名学生进入第二轮面试?
(3)在(2)的前提下,学校决定从6名学生中随机抽取2名学生接受甲考官的面试,求第4组至少有1名学生被甲考官面试的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高校在2016年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组,得到的频率分布表如下表所示.
组号 | 分组 | 频数 | 频率 |
第1组 |
| 5 | 0.050 |
第2组 |
| n | 0.350 |
第3组 |
| 30 | p |
第4组 |
| 20 | 0.200 |
第5组 |
| 10 | 0.100 |
合计 | 100 | 1.000 |
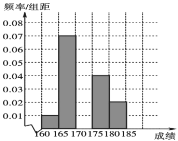
(1)求频率分布表中n,p的值,并估计该组数据的中位数(保留l位小数);
(2)为了能选拔出最优秀的学生,高校决定在笔试成绩高的第3、4、5组中用分层抽样的方法抽取6名学生进入第二轮面试,则第3、4、5组每组各抽取多少名学生进入第二轮面试?
(3)在(2)的前提下,学校决定从6名学生中随机抽取2名学生接受甲考官的面试,求第4组至少有1名学生被甲考官面试的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,
,![]() 且满足:
且满足:![]()
(1)证明:![]() 是等比数列,并求数列
是等比数列,并求数列![]() 的通项公式.
的通项公式.
(2)设![]() ,若数列
,若数列![]() 是等差数列,求实数
是等差数列,求实数![]() 的值;
的值;
(3)在(2)的条件下,设![]() 记数列
记数列![]() 的前
的前![]() 项和为
项和为![]() ,若对任意的
,若对任意的![]() 存在实数
存在实数![]() ,使得
,使得![]() ,求实数
,求实数![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国古代数学名著《九章算术》中有这样一个问題:今有牛、马、羊食人苗,苗主责之粟五斗,羊主曰:“我羊食半马、“马主曰:“我马食半牛,”今欲衰偿之,问各出几何?此问题的译文是:今有牛、马、羊吃了别人的禾苗,禾苗主人要求赔偿5斗粟、羊主人说:“我羊所吃的禾苗只有马的一半,”马主人说:“我马所吃的禾苗只有牛的一半,“打算按此比例偿还,他们各应偿还多少?该问题中,1斗为10升,则马主人应偿还( )升粟?
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个盒子里装有大小均匀的6个小球,其中有红色球4个,编号分别为1,2,3,4;白色球2个,编号分别为4,5,从盒子中任取3个小球(假设取到任何—个小球的可能性相同).
(1)求取出的3个小球中,含有编号为4的小球的概率;
(2)在取出的3个小球中,小球编号的最大值设为![]() ,求随机变量
,求随机变量![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com