
| A�� | 4x��y=0 | B�� | x��4y=0 | C�� | 2x��y=0 | D�� | x��2y=0 |
���� ��Բ�ķ������Բ�����꣬���D�����꣬��������ʽ���D�����꣬��|MF|=3|DF|�����M�����꣬�ٰ�M���������˫���߷�����ô𰸣�
��� �⣺��x2+y2-$\frac{2c}{3}$y+$\frac{{a}^{2}}{9}$=0����x2+��y-$\frac{c}{3}$��2=$\frac{{b}^{2}}{9}$��
���Բ��Բ������Ϊ��0��$\frac{c}{3}$�����뾶Ϊ$\frac{b}{3}$��
���е�D��x0��y0����y0��0����
����x2+y2-$\frac{2c}{3}$y+$\frac{{a}^{2}}{9}$=0�루x0��y0-c��•��x0��y0-$\frac{c}{3}$��=0��
��ã�x0=$\frac{b\sqrt{3{c}^{2}+{a}^{2}}}{6c}$��y0=$\frac{3{c}^{2}-{a}^{2}}{6c}$��
��D��$\frac{b\sqrt{3{c}^{2}+{a}^{2}}}{6c}$��$\frac{3{c}^{2}-{a}^{2}}{6c}$����
��|MF|=3|DF|����$\overrightarrow{MF}$=3$\overrightarrow{DF}$����M��$\frac{b\sqrt{3{c}^{2}+{a}^{2}}}{2c}$��-$\frac{{a}^{2}+{c}^{2}}{2c}$ ����
���� ˫���ߦ���$\frac{{y}^{2}}{{a}^{2}}$-$\frac{{x}^{2}}{{b}^{2}}$=1��a��0��b��0��������b=2a����˫���ߧ��Ľ����߷���Ϊy=��$\frac{1}{2}$x��
��ѡ��D��
���� ���⿼����˫���ߵļ������ʣ�������Բ��Բ����Ĺ�ϵ��������ѧ���ļ������������е��⣮


 ��У��ʦ������ҵ���Ӻ����Ծ�ϵ�д�
��У��ʦ������ҵ���Ӻ����Ծ�ϵ�д� ȫ�̽��ϵ�д�
ȫ�̽��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��ֲ���Ҫ���� | B�� | ��Ҫ��������� | ||
| C�� | ��Ҫ���� | D�� | �Ȳ����Ҳ����Ҫ���� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
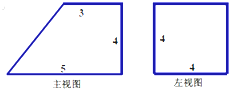
| A�� | 36 | B�� | 48 | C�� | 64 | D�� | 72 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
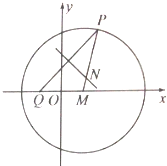 ��ͼ��PΪԲM����x-$\sqrt{3}$��2+y2=24�ϵĶ��㣬����Q��-$\sqrt{3}$��0�����߶�PQ�Ĵ�ֱƽ���߽��߶�MP�ڵ�N��
��ͼ��PΪԲM����x-$\sqrt{3}$��2+y2=24�ϵĶ��㣬����Q��-$\sqrt{3}$��0�����߶�PQ�Ĵ�ֱƽ���߽��߶�MP�ڵ�N���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | x1��x2 | B�� | x1��x2 | C�� | x1+x2��0 | D�� | x1+x2��0 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com