
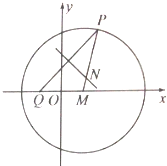
 如图,P为圆M:(x-$\sqrt{3}$)2+y2=24上的动点,定点Q(-$\sqrt{3}$,0),线段PQ的垂直平分线交线段MP于点N.
如图,P为圆M:(x-$\sqrt{3}$)2+y2=24上的动点,定点Q(-$\sqrt{3}$,0),线段PQ的垂直平分线交线段MP于点N.分析 (Ⅰ)|NP|=|NQ|,可得|NM|+|NQ|=|MP|=2$\sqrt{6}$>2$\sqrt{3}$=|MQ|,故点N的轨迹是以M、Q为焦点,长轴长等于2$\sqrt{6}$的椭圆,且c=$\sqrt{3}$,即得椭圆C的方程;
(Ⅱ)分类讨论,当切线l垂直坐标轴时,|OA||OB|=4;当切线不垂直坐标轴时,设方程为y=kx+m(k≠0),圆心到直线的距离d=$\frac{|m|}{\sqrt{{k}^{2}+1}}$=$\sqrt{2}$,得m2=2+2k2.直线与椭圆方程联立得(2k2+1)x2+4kmx+2m2-6=0,得出|OA||OB|=$\sqrt{2}$|AB|,即可求|OA|•|OB|的最大值.
解答 解:(Ⅰ)∵|NP|=|NQ|,∴|NM|+|NQ|=|MP|=2$\sqrt{6}$>2$\sqrt{3}$=|MQ|,
故点N的轨迹是以M、Q为焦点,长轴长等于2$\sqrt{6}$的椭圆,且c=$\sqrt{3}$,
∴b=$\sqrt{3}$
∴椭圆的方程为$\frac{{x}^{2}}{6}+\frac{{y}^{2}}{3}$=1;
(Ⅱ)(1)当切线l垂直坐标轴时,|OA||OB|=4;
(2)当切线不垂直坐标轴时,设方程为y=kx+m(k≠0),A(x1,y1),B(x2,y2),
由圆心到直线的距离d=$\frac{|m|}{\sqrt{{k}^{2}+1}}$=$\sqrt{2}$,得m2=2+2k2.
直线与椭圆方程联立得(2k2+1)x2+4kmx+2m2-6=0.
∴x1+x2=-$\frac{4km}{2{k}^{2}+1}$,x1x2=$\frac{2{m}^{2}-6}{2{k}^{2}+1}$,
∴x1x2+y1y2=(k2+1)x1x2+km(x1+x2)+m2=$\frac{3{m}^{2}-6-6{k}^{2}}{2{k}^{2}+1}$=0,
∴∠AOB=90°,
∴|OA||OB|=$\sqrt{2}$|AB|,
∵|AB|=$\sqrt{1+{k}^{2}}|{x}_{1}-{x}_{2}|$=$\frac{2\sqrt{(1+{k}^{2})(8{k}^{2}+2)}}{2{k}^{2}+1}$.
令t=k2,则|AB|=2$\sqrt{2+\frac{2}{4t+\frac{1}{t}+4}}$≤3,
当且仅当k=±$\frac{\sqrt{2}}{2}$时,等号成立,
∴|OA||OB|≤3$\sqrt{2}$,
综上所述,|OA|•|OB|的最大值为3$\sqrt{2}$.
点评 本题考查点的轨迹方程的求法,考查韦达定理、基本不等式、直线与圆的位置关系,解题时要认真审题,注意积累解题方法,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4x±y=0 | B. | x±4y=0 | C. | 2x±y=0 | D. | x±2y=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{3}$ | B. | $\frac{1}{3}$ | C. | -$\frac{1}{3}$或1 | D. | $\frac{1}{3}$或-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-2,4) | B. | (4,5) | C. | (-3,-2) | D. | (2,4) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com