
【题目】定义在R上的偶函数f(x)满足f(e+x)=f(e﹣x),且f(0)=0,当x∈(0,e]时,f(x)=lnx已知方程![]() 在区间[﹣e,3e]上所有的实数根之和为3ea,将函数
在区间[﹣e,3e]上所有的实数根之和为3ea,将函数![]() 的图象向右平移a个单位长度,得到函数h(x)的图象,,则h(7)=_____.
的图象向右平移a个单位长度,得到函数h(x)的图象,,则h(7)=_____.
【答案】![]()
【解析】
根据题意可知函数f(x)是一个周期为2e的偶函数,即可作出函数f(x)在[﹣e,3e]上的图象,由方程的根与两函数图象交点的横坐标的关系可求得![]() 的值,再利用二倍角公式化简函数
的值,再利用二倍角公式化简函数![]() ,然后根据平移法则即可求得
,然后根据平移法则即可求得![]() ,从而求得
,从而求得![]() .
.
因为f(e+x)=f(e﹣x),所以f(x)关于x=e对称,又因为偶函数f(x),
所以f(x)的周期为2e.
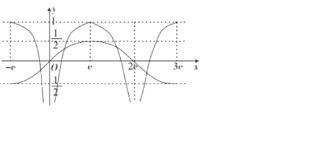
当x∈(0,e]时,f(x)=lnx,于是可作出函数f(x)在[﹣e,3e]上的图象如图所示,
方程![]() 的实数根是函数y=f(x)与函数
的实数根是函数y=f(x)与函数![]() 的交点的横坐标,
的交点的横坐标,
由图象的对称性可知,两个函数在[﹣e,3e]上有4个交点,且4个交点的横坐标之和为4e,所以4e=3ea,故a![]() ,
,
因为![]() ,
,
所以![]() ,
,
故![]() .
.
故答案为:![]() .
.


科目:高中数学 来源: 题型:
【题目】销售某种活海鲜,根据以往的销售情况,按日需量![]() (公斤)属于[0,100),[100,200),[200,300),[300,400),[400,500]进行分组,得到如图所示的频率分布直方图.这种海鲜经销商进价成本为每公斤20元,当天进货当天以每公斤30元进行销售,当天未售出的须全部以每公斤10元卖给冷冻库.某海鲜产品经销商某天购进了300公斤这种海鲜,设当天利润为
(公斤)属于[0,100),[100,200),[200,300),[300,400),[400,500]进行分组,得到如图所示的频率分布直方图.这种海鲜经销商进价成本为每公斤20元,当天进货当天以每公斤30元进行销售,当天未售出的须全部以每公斤10元卖给冷冻库.某海鲜产品经销商某天购进了300公斤这种海鲜,设当天利润为![]() 元.
元.

(I)求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(II)结合直方图估计利润![]() 不小于800元的概率.
不小于800元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 、
、![]() 为曲线
为曲线![]() 上两点,
上两点,![]() 与
与![]() 的横坐标之和为
的横坐标之和为![]() .
.
(1)求直线![]() 的斜率;
的斜率;
(2)设弦![]() 的中点为
的中点为![]() ,过点
,过点![]() 、
、![]() 分别作抛物线的切线,则两切线的交点为
分别作抛物线的切线,则两切线的交点为![]() ,过点
,过点![]() 作直线
作直线![]() ,交抛物线于
,交抛物线于![]() 、
、![]() 两点,连接
两点,连接![]() 、
、![]() .证明:
.证明:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《西游记》《三国演义》《水浒传》和《红楼梦》是中国古典文学瑰宝,并称为中国古典小说四大名著.某中学为了解本校学生阅读四大名著的情况,随机调查了100名学生,其中阅读过《西游记》的学生有70位,只阅读过《红楼梦》的学生有20位,则既没阅读过《西游记》也没阅读过《红楼梦》的学生人数与该校学生总数比值的估计值为( )
A.0.1B.0.2C.0.3D.0.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将n2个数排成n行n列的一个数阵,如图:该数阵第一列的n个数从上到下构成以m为公差的等差数列,每一行的n个数从左到右构成以m为公比的等比数列(其中m>0).已知a11=2,a13=a61+1,记这n2个数的和为S.下列结论正确的有( )
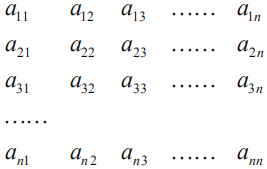
A.m=3B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了整顿道路交通秩序,某地考虑对行人闯红灯进行处罚.为了更好地了解市民的态度,在普通人中随机抽取200人进行调查,当不处罚时,有80人会闯红灯,处罚时,得到如下数据:
处罚金额 | 5 | 10 | 15 | 20 |
会闯红灯的人数 | 50 | 40 | 20 | 0 |
若用表中数据所得频率代替概率.
(1)当处罚金定为10元时,行人闯红灯的概率会比不进行处罚降低多少?
(2)将选取的200人中会闯红灯的市民分为两类:![]() 类市民在罚金不超过10元时就会改正行为;
类市民在罚金不超过10元时就会改正行为;![]() 类是其它市民.现对
类是其它市民.现对![]() 类与
类与![]() 类市民按分层抽样的方法抽取4人依次进行深度问卷,则前两位均为
类市民按分层抽样的方法抽取4人依次进行深度问卷,则前两位均为![]() 类市民的概率是多少?
类市民的概率是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数![]() (其中
(其中![]() )的部分图象如图所示,把函数
)的部分图象如图所示,把函数![]() 的图像向右平移
的图像向右平移![]() 个单位长度,再向下平移1个单位,得到函数
个单位长度,再向下平移1个单位,得到函数![]() 的图像.
的图像.

(1)当![]() 时,求
时,求![]() 的值域
的值域
(2)令![]() ,若对任意
,若对任意![]() 都有
都有![]() 恒成立,求
恒成立,求![]() 的最大值
的最大值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为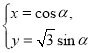 (
(![]() 为参数).以坐标原点为极点,以
为参数).以坐标原点为极点,以![]() 轴的正半轴为极轴,建立极坐标系,曲线
轴的正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出![]() 的普通方程和
的普通方程和![]() 的直角坐标方程;
的直角坐标方程;
(2)设点![]() 在
在![]() 上,点
上,点![]() 在
在![]() 上,求
上,求![]() 的最小值及此时
的最小值及此时![]() 的直角坐标.
的直角坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】由我国引领的5G时代已经到来,5G的发展将直接带动包括运营、制造、服务在内的通信行业整体的快速发展,进而对![]() 增长产生直接贡献,并通过产业间的关联效应和波及效应,间接带动国民经济各行业的发展,创造岀更多的经济增加值.如图是某单位结合近年数据,对今后几年的5G经济产出所做的预测.结合下图,下列说法正确的是( )
增长产生直接贡献,并通过产业间的关联效应和波及效应,间接带动国民经济各行业的发展,创造岀更多的经济增加值.如图是某单位结合近年数据,对今后几年的5G经济产出所做的预测.结合下图,下列说法正确的是( )
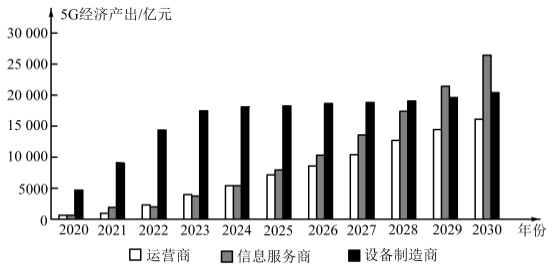
A.5G的发展带动今后几年的总经济产出逐年增加
B.设备制造商的经济产出前期增长较快,后期放缓
C.设备制造商在各年的总经济产出中一直处于领先地位
D.信息服务商与运营商的经济产出的差距有逐步拉大的趋势
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com