练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】销售某种活海鲜，根据以往的销售情况，按日需量（公斤）属于[0，100)，[100，200)，[200，300)，[300，400)，[400，500]进行分组，得到如图所示的频率分布直方图．这种海鲜经销商进价成本为每公斤20元，当天进货当天以每公斤30元进行销售，当天未售出的须全部以每公斤10元卖给冷冻库．某海鲜产品经销商某天购进了300公斤这种海鲜，设当天利润为元．

    （I）求关于的函数关系式；

    （II）结合直方图估计利润不小于800元的概率．

    【答案】（I）；（II）0.072.

    【解析】

    （I）利润=（售价-成本）数量，分段表示即可.

    （II）由（I）知时，的范围，之后结合直方图可求概率.

    （Ⅰ）当日需求量不低于公斤时，利润元；

    当日需求量不足公斤时，利润（元）；

    故．

    （Ⅱ）由得，，

    ∴

    ．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】在直角坐标系中，已知圆圆心为，过点且斜率为的直线与圆相交于不同的两点、．

    （）求的取值范围；

    （）是否存在常数，使得向量与共线？如果存在，求值；如果不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】考察下列无穷数列，判断是否有极限，若有，求出极限；若没有，请说明理由．

    （1）

    （2）

    （3）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知在等比数列{an}中，＝2，，＝128，数列{bn}满足b1＝1，b2＝2，且{}为等差数列．

    （1）求数列{an}和{bn}的通项公式；

    （2）求数列{bn}的前n项和．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在平面直角坐标系xOy中，直线l的参数方程为（t为参数），以坐标原点为极点，x轴的非负半轴为极轴且取相同的单位长度建立极坐标系，已知曲线C的极坐标方程为，且直线l经过曲线C的左焦点F．

    （1）求直线l的普通方程；

    （2）设曲线C的内接矩形的周长为L，求L的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在四棱锥P-ABCD中，ABCD为梯形，AB//CD，BC⊥AB，AB=2，BC=，CD=PC=。

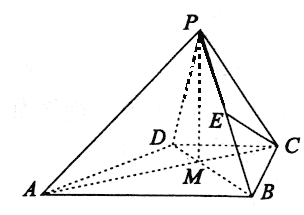
    （I）点E在线段PB上，满足CE//平面PAD，求的值。

    （II）已知AC与BD的交点为M，若PM=1，且平面PAC⊥平面ABCD，求二面角P-BC-M平面角的余弦值。

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知两个不同的单位向量与之间满足关系：，其中．

    （1）若，求的解析式；

    （2）能否和垂直？能否和平行？若不能，则说明理由；若能，则求出对应的k值；

    （3）求与夹角的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在斜三棱柱中，AB=1，AC=2，，AB⊥AC，底面ABC.

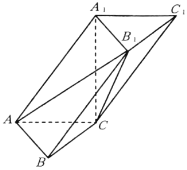
    （1）求直线与平面所成角的正弦值；

    （2）求平面与平面所成锐二面角的余弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （1）若函数在上是增函数，求实数的取值范围；

    （2）若函数在上的最小值为3，求实数的值.

    查看答案和解析>>

    同步练习册答案