
【题目】考察下列无穷数列,判断是否有极限,若有,求出极限;若没有,请说明理由.
(1)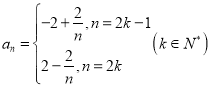
(2)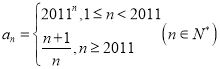
(3)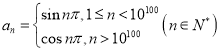
科目:高中数学 来源: 题型:
【题目】某高中志愿者部有男志愿者6人,女志愿者4人,这些人要参加元旦联欢会的服务工作. 从这些人中随机抽取4人负责舞台服务工作,另外6人负责会场服务工作.
(Ⅰ)设![]() 为事件:“负责会场服务工作的志愿者中包含女志愿者
为事件:“负责会场服务工作的志愿者中包含女志愿者![]() 但不包含男志愿者
但不包含男志愿者![]() ”,求事件
”,求事件![]() 发生的概率.
发生的概率.
(Ⅱ)设![]() 表示参加舞台服务工作的女志愿者人数,求随机变量
表示参加舞台服务工作的女志愿者人数,求随机变量![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于给定数列![]() ,如果存在实常数
,如果存在实常数![]() 使得
使得![]() 对于任意
对于任意![]() 都成立,我们称数列
都成立,我们称数列![]() 是“M类数列”.
是“M类数列”.
(1)若![]() ,数列
,数列![]() 是否为“M类数列”?若是,指出它对应的实常数
是否为“M类数列”?若是,指出它对应的实常数![]() ;若不是,请说明理由;
;若不是,请说明理由;
(2)证明:若数列![]() 是“M类数列”,则数列
是“M类数列”,则数列![]() 也是“M类数列”.
也是“M类数列”.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在数列![]() 中,若
中,若![]() 是正整数,且
是正整数,且![]() ,…,则称
,…,则称![]() 为“绝对差数列”.
为“绝对差数列”.
(1)举出一个前5项不为零的“绝对差数列”(只要求写出前10项);
(2)若“绝对差数列”![]() 中,
中,![]() ,数列
,数列![]() 满足
满足![]() ,
,![]() ,…,分别判断当
,…,分别判断当![]() 时,
时,![]() 与
与![]() 的极限是否存在?如果存在,求出其极限值.
的极限是否存在?如果存在,求出其极限值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某电器商场销售的彩电、U盘和![]() 播放器三种产品.该商场的供货渠道主要是甲、乙两个品牌的二级代理商.今年9月份,该商场从每个代理商处各购得彩电100台、U盘52个、
播放器三种产品.该商场的供货渠道主要是甲、乙两个品牌的二级代理商.今年9月份,该商场从每个代理商处各购得彩电100台、U盘52个、![]() 播放器180台.而10月份,该商场从每个代理商处购得的产品数量都是9月份的1.5倍.现知甲、乙两个代理商给出的产品单价(元)如下页表中所示:
播放器180台.而10月份,该商场从每个代理商处购得的产品数量都是9月份的1.5倍.现知甲、乙两个代理商给出的产品单价(元)如下页表中所示:
彩电 | U盘 |
| |
甲代理商单价(元) | 2350 | 1200 | 750 |
乙代理商单价(元) | 2100 | 920 | 700 |
(1)计算![]() ,并指出结果的实际意义;
,并指出结果的实际意义;
(2)用矩阵求该商场在这两个月中分别支付给两个代理商的购货费用.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在等比数列{an}中,![]() =2,,
=2,,![]() =128,数列{bn}满足b1=1,b2=2,且{
=128,数列{bn}满足b1=1,b2=2,且{![]() }为等差数列.
}为等差数列.
(1)求数列{an}和{bn}的通项公式;
(2)求数列{bn}的前n项和.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线l的参数方程为 (t为参数),以坐标原点为极点,x轴的非负半轴为极轴且取相同的单位长度建立极坐标系,已知曲线C的极坐标方程为
(t为参数),以坐标原点为极点,x轴的非负半轴为极轴且取相同的单位长度建立极坐标系,已知曲线C的极坐标方程为![]() ,且直线l经过曲线C的左焦点F.
,且直线l经过曲线C的左焦点F.
(1)求直线l的普通方程;
(2)设曲线C的内接矩形的周长为L,求L的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】销售某种活海鲜,根据以往的销售情况,按日需量![]() (公斤)属于[0,100),[100,200),[200,300),[300,400),[400,500]进行分组,得到如图所示的频率分布直方图.这种海鲜经销商进价成本为每公斤20元,当天进货当天以每公斤30元进行销售,当天未售出的须全部以每公斤10元卖给冷冻库.某海鲜产品经销商某天购进了300公斤这种海鲜,设当天利润为
(公斤)属于[0,100),[100,200),[200,300),[300,400),[400,500]进行分组,得到如图所示的频率分布直方图.这种海鲜经销商进价成本为每公斤20元,当天进货当天以每公斤30元进行销售,当天未售出的须全部以每公斤10元卖给冷冻库.某海鲜产品经销商某天购进了300公斤这种海鲜,设当天利润为![]() 元.
元.

(I)求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(II)结合直方图估计利润![]() 不小于800元的概率.
不小于800元的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com