
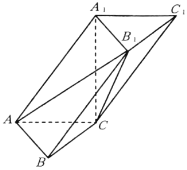
【题目】如图,在斜三棱柱![]() 中,AB=1,AC=2,
中,AB=1,AC=2,![]() ,AB⊥AC,
,AB⊥AC,![]() 底面ABC.
底面ABC.
(1)求直线![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(2)求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
【答案】(1)![]() .(2)
.(2)![]()
【解析】
(1)以A为原点,![]() 分别为x轴,y轴的正方向建立空间直角坐标系
分别为x轴,y轴的正方向建立空间直角坐标系![]() ,求得向量
,求得向量![]() 的坐标,再根据
的坐标,再根据![]() 底面
底面![]() ,得到
,得到![]() ,又
,又![]() ,由线面垂直的判定定理得到
,由线面垂直的判定定理得到![]() 平面
平面![]() ,从而
,从而![]() 是平面
是平面![]() 的一个法向量,然后由
的一个法向量,然后由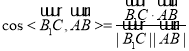 求解.
求解.
(2)由(1)知![]() 是平面
是平面![]() 的一个法向量,再求得平面
的一个法向量,再求得平面![]() 的一个法向量
的一个法向量![]() ,然后由
,然后由![]() 求解.
求解.
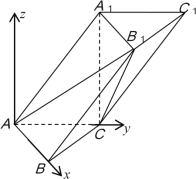
(1)以A为原点,![]() 分别为x轴,y轴的正方向建立如图所示的空间直角坐标系
分别为x轴,y轴的正方向建立如图所示的空间直角坐标系![]() ,
,
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
则![]() ,
,
∵![]() 底面
底面![]() ,
,![]() 底面
底面![]() ,
,
∴![]() ,
,
又∵![]() ,
,![]() ,
,
![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() ,
,
∴![]() 是平面
是平面![]() 的一个法向量,
的一个法向量,
∴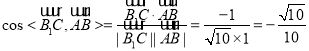 ,
,
故所求直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]()
(2)![]() ,
,![]() ,
,
设![]() 为平面
为平面![]() 的一个法向量,
的一个法向量,
则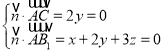 ,
,
令![]() ,得
,得![]() ,
,
得平面![]() 的一个法向量为
的一个法向量为![]() ,
,
又由(1)得![]() 是平面
是平面![]() 的一个法向量,
的一个法向量,
∴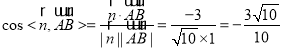 ,
,
故所求面![]() 与平面
与平面![]() 所成锐二面角的余弦值为
所成锐二面角的余弦值为![]() .
.


 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案科目:高中数学 来源: 题型:
【题目】在数列![]() 中,若
中,若![]() 是正整数,且
是正整数,且![]() ,…,则称
,…,则称![]() 为“绝对差数列”.
为“绝对差数列”.
(1)举出一个前5项不为零的“绝对差数列”(只要求写出前10项);
(2)若“绝对差数列”![]() 中,
中,![]() ,数列
,数列![]() 满足
满足![]() ,
,![]() ,…,分别判断当
,…,分别判断当![]() 时,
时,![]() 与
与![]() 的极限是否存在?如果存在,求出其极限值.
的极限是否存在?如果存在,求出其极限值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】销售某种活海鲜,根据以往的销售情况,按日需量![]() (公斤)属于[0,100),[100,200),[200,300),[300,400),[400,500]进行分组,得到如图所示的频率分布直方图.这种海鲜经销商进价成本为每公斤20元,当天进货当天以每公斤30元进行销售,当天未售出的须全部以每公斤10元卖给冷冻库.某海鲜产品经销商某天购进了300公斤这种海鲜,设当天利润为
(公斤)属于[0,100),[100,200),[200,300),[300,400),[400,500]进行分组,得到如图所示的频率分布直方图.这种海鲜经销商进价成本为每公斤20元,当天进货当天以每公斤30元进行销售,当天未售出的须全部以每公斤10元卖给冷冻库.某海鲜产品经销商某天购进了300公斤这种海鲜,设当天利润为![]() 元.
元.

(I)求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(II)结合直方图估计利润![]() 不小于800元的概率.
不小于800元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】①![]() ;②
;②![]() ;③
;③![]() (
(![]() 为常数)这
为常数)这![]() 个条件中选择
个条件中选择![]() 个条件,补全下列试题后完成解答,设等差数列
个条件,补全下列试题后完成解答,设等差数列![]() 的前
的前![]() 项和为
项和为![]() ,若数列
,若数列![]() 的各项均为正整数,且满足公差
的各项均为正整数,且满足公差![]() ,____________.
,____________.
(1)求数列![]() 的通项公式;
的通项公式;
(2)令![]() ,求数列
,求数列![]() 的前
的前![]() 项的和.
项的和.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂连续6天对新研发的产品按事先拟定的价格进行试销,得到一组数据![]() 如下表所示
如下表所示
日期 | 4月1日 | 4月2日 | 4月3日 | 4月4日 | 4月5日 | 4月6日 |
试销价 | 9 | 11 | 10 | 12 | 13 | 14 |
产品销量 | 40 | 32 | 29 | 35 | 44 |
|
(1)试根据4月2日、3日、4日的三组数据,求![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ,并预测4月6日的产品销售量
,并预测4月6日的产品销售量![]() ;
;
(2)若选取两组数据确定回归方程,求选取得两组数据恰好是不相邻两天的事件![]() 的概率.
的概率.
参考公式:![]()
其中
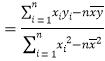 ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年12月18日上午10时,在人民大会堂举行了庆祝改革开放40周年大会.40年众志成城,40年砥砺奋进,40年春风化雨,中国人民用双手书写了国家和民族发展的壮丽史诗.会后,央视媒体平台,收到了来自全国各地的纪念改革开放40年变化的老照片,并从众多照片中抽取了100张照片参加“改革开放40年图片展”,其作者年龄集中在![]() 之间,根据统计结果,做出频率分布直方图如下:
之间,根据统计结果,做出频率分布直方图如下:

(Ⅰ)求这100位作者年龄的样本平均数![]() 和样本方差
和样本方差![]() (同一组数据用该区间的中点值作代表);
(同一组数据用该区间的中点值作代表);
(Ⅱ)由频率分布直方图可以认为,作者年龄X服从正态分布![]() ,其中
,其中![]() 近似为样本平
近似为样本平
均数![]() ,
,![]() 近似为样本方差
近似为样本方差![]() .
.
(i)利用该正态分布,求![]() ;
;
(ii)央视媒体平台从年龄在![]() 和
和![]() 的作者中,按照分层抽样的方法,抽出了7人参加“纪念改革开放40年图片展”表彰大会,现要从中选出3人作为代表发言,设这3位发言者的年龄落在区间
的作者中,按照分层抽样的方法,抽出了7人参加“纪念改革开放40年图片展”表彰大会,现要从中选出3人作为代表发言,设这3位发言者的年龄落在区间![]() 的人数是Y,求变量Y的分布列和数学期望.附:
的人数是Y,求变量Y的分布列和数学期望.附:![]() ,若
,若![]() ,则
,则![]() ,
,![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com