
【题目】某工厂连续6天对新研发的产品按事先拟定的价格进行试销,得到一组数据![]() 如下表所示
如下表所示
日期 | 4月1日 | 4月2日 | 4月3日 | 4月4日 | 4月5日 | 4月6日 |
试销价 | 9 | 11 | 10 | 12 | 13 | 14 |
产品销量 | 40 | 32 | 29 | 35 | 44 |
|
(1)试根据4月2日、3日、4日的三组数据,求![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ,并预测4月6日的产品销售量
,并预测4月6日的产品销售量![]() ;
;
(2)若选取两组数据确定回归方程,求选取得两组数据恰好是不相邻两天的事件![]() 的概率.
的概率.
参考公式:![]()
其中
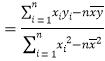 ,
,![]()
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】在四棱锥P-ABCD中,ABCD为梯形,AB//CD,BC⊥AB,AB=2![]() ,BC=
,BC=![]() ,CD=PC=
,CD=PC=![]() 。
。
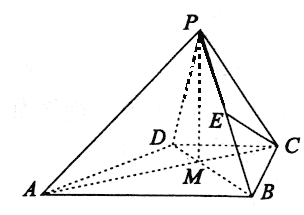
(I)点E在线段PB上,满足CE//平面PAD,求![]() 的值。
的值。
(II)已知AC与BD的交点为M,若PM=1,且平面PAC⊥平面ABCD,求二面角P-BC-M平面角的余弦值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图![]() ,已知
,已知![]() 是边长为6的等边三角形,点D、E分别是边AB、AC上的点,且满足
是边长为6的等边三角形,点D、E分别是边AB、AC上的点,且满足![]() ,如图
,如图![]() ,将
,将![]() 沿DE折成四棱锥
沿DE折成四棱锥![]() ,且有平面
,且有平面![]() 平面BCED.
平面BCED.

![]() 求证:
求证:![]() 平面BCED;
平面BCED;
![]() 记
记![]() 的中点为M,求二面角
的中点为M,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在斜三棱柱![]() 中,AB=1,AC=2,
中,AB=1,AC=2,![]() ,AB⊥AC,
,AB⊥AC,![]() 底面ABC.
底面ABC.
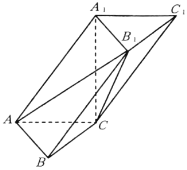
(1)求直线![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(2)求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 满足
满足![]() (
(![]() ),
),![]() (
(![]() ),则下列说法中错误的是( )
),则下列说法中错误的是( )
A.若![]() ,则数列
,则数列![]() 为递增数列
为递增数列
B.若数列![]() 为递增数列,则
为递增数列,则![]()
C.存在实数![]() ,使数列
,使数列![]() 为常数数列
为常数数列
D.存在实数![]() ,使
,使![]() 恒成立
恒成立
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() ,若曲线
,若曲线![]() 与曲线
与曲线![]() 关于直线
关于直线![]() 对称.
对称.
(1)求曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)在以![]() 为极点,
为极点,![]() 轴的正半轴为极轴的极坐标系中,射线
轴的正半轴为极轴的极坐标系中,射线![]() 与
与![]() 的异于极点的交点为
的异于极点的交点为![]() ,与
,与![]() 的异于极点的交点为
的异于极点的交点为![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的离心率为
的离心率为![]() ,圆
,圆![]() :
: ![]() 与
与![]() 轴交于点
轴交于点![]() 、
、![]() ,
, ![]() 为椭圆
为椭圆![]() 上的动点,
上的动点, ![]() ,
, ![]() 面积最大值为
面积最大值为![]() .
.
(1)求圆![]() 与椭圆
与椭圆![]() 的方程;
的方程;
(2)圆![]() 的切线
的切线![]() 交椭圆于点
交椭圆于点![]() 、
、![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com