
分析 (1)根据题设条件,可求a1,a2,a3的值,猜想{an}的通项公式.
(2)利用数学归纳法的证明步骤对这个猜想加以证明.
解答 解:(Ⅰ)${a_1}=\frac{3}{2}$,${a_2}=\frac{7}{4}$,${a_3}=\frac{15}{8}$,猜测 ${a_n}=2-\frac{1}{2^n}$,
(Ⅱ)证明:①由(1)知当n=1时,命题成立;
②假设n=k时,命题成立,即 ${a_k}=2-\frac{1}{2^k}$,
当n=k+1时,a1+a2+…+ak+ak+1+ak+1=2(k+1)+1,
且a1+a2+…+ak=2k+1-ak∴2k+12k+1-ak+2ak+1=2(k+1)+1=2k+3,
∴$2{a_{k+1}}=2+2-\frac{1}{2^k}$,${a_{k+1}}=2-\frac{1}{{{2^{k+1}}}}$,
即当n=k+1时,命题成立.
根据①②得n∈N*,${a_n}=2-\frac{1}{2^n}$都成立
点评 此题主要考查归纳法的证明,归纳法一般三个步骤:(1)验证n=1成立;(2)假设n=k成立;(3)利用已知条件证明n=k+1也成立,从而求证,这是数列的通项一种常用求解的方法


 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案科目:高中数学 来源: 题型:解答题
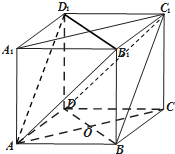 在正方体ABCD-A1B1C1D1中,O是底面ABCD对角线的交点.
在正方体ABCD-A1B1C1D1中,O是底面ABCD对角线的交点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (2-$\sqrt{2}$,1] | B. | (2-$\sqrt{2}$,2+$\sqrt{2}$] | C. | (-∞,2-$\sqrt{2}$)∪(2+$\sqrt{2}$,+∞) | D. | [-1,$\sqrt{2}$-2) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
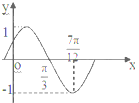 把函数y=Asin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的图象向左平移$\frac{π}{3}$个单位得到y=f(x)的图象(如图),则2A-ω+φ=( )
把函数y=Asin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的图象向左平移$\frac{π}{3}$个单位得到y=f(x)的图象(如图),则2A-ω+φ=( )| A. | $-\frac{π}{3}$ | B. | $\frac{π}{3}$ | C. | $-\frac{π}{6}$ | D. | $\frac{π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,$\frac{1}{2}$] | B. | [$\frac{1}{2}$,+∞) | C. | (-2,$\frac{1}{2}$] | D. | [$\frac{1}{2}$,3) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
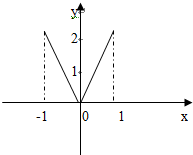
| A. | y=f(|x|) | B. | y=|f(x)| | C. | y=f(-|x|) | D. | y=-f(|x|) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
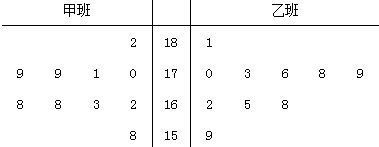
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com