练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    5．已知函数f（x）=$\left\{\begin{array}{l}{-2x，-1≤x≤0}\\{\sqrt{x}，0＜x≤1}\end{array}\right.$，则图中的图象对应的函数在下列给出的四个解析式中，只可能是（　　）
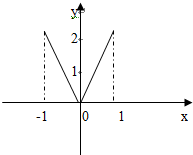
    A．y=f（|x|）B．y=|f（x）|C．y=f（-|x|）D．y=-f（|x|）

    分析 画出分段函数的图象，结合给出的函数图象可得对应的解析式．

    解答 解：作出函数f（x）=$\left\{\begin{array}{l}{-2x，-1≤x≤0}\\{\sqrt{x}，0＜x≤1}\end{array}\right.$的图象如图，

    则

    对应的函数解析式为y=f（-|x|）．
    故选：C．

    点评 本题考查函数的图象，考查了函数的图象变换，是中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    15．已知f（x）是定义在[5-2a，a]上的奇函数，且当x∈[-5，0）时，f（x）=-x （4-x）．
    （1）f（x）的解析式；
    （2）求f（x）的最值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    16．已知数列{an}满足Sn+an=2n+1（n∈N*），其中Sn表示数列{an}的前n项和．
    （Ⅰ）求出a1，a2，a3，并推测数列{an}的表达式；
    （Ⅱ）用数学归纳法证明所得的结论．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    13．圆（x+2）2+y2=4与圆x2+y2-2x-2y+1=0（　　）
    A．内切B．相交C．外切D．相离

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    20．以下求方程x5+x3+x2-1=0在[0，1]之间近似根的算法是（　　）
    x1←0
    x2←1
    x←（x1+x2）/2
    c←0.00001
    While x2-x1＞c
    If x5+x3+x2-1＞0then
    x2←x
    Else
    x1←x
    End if
    x=（x1+x2）/2
    End while
    Print x．
    A．辗转相除法B．二分法C．更相减损术D．秦九韶算法

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    10．化简：$\frac{5}{6}$a${\;}^{\frac{1}{2}}$b${\;}^{-\frac{1}{2}}$×（-3a${\;}^{\frac{1}{6}}$b-1）÷（4a${\;}^{\frac{2}{3}}$b-3）${\;}^{\frac{1}{2}}$=-$\frac{5}{4}$${a}^{\frac{1}{3}}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    17．已知tanx=2，则$\frac{3cosx+2sinx}{4cosx-5sinx}$=-$\frac{7}{6}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    14．某人种植一种经济作物，根据以往的年产量数据，得到年产量频率分布直方图如图所示，以各区间中点值作为该区间的年产量，得到平均年产量为455kg，已知当年产量低于350kg时，单位售价为20元/kg，若当年产量不低于350kg而低于550时，单位售价为15元/kg，当年产量不低于550kg时，单位售价为10元/kg．
    （1）求图中a，b的值；
    （2）试估计年销售额的期望是多少？

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    15．关于直线a，b以及平面M，N，下列命题中正确的是（　　）
    A．若a∥M，b∥M，则a∥bB．若a∥M，b⊥a，则b⊥M
    C．若b?M，且b⊥a，则a⊥MD．若a⊥M，a∥N，则 M⊥N

    查看答案和解析>>

    同步练习册答案