
分析 利用有理数指数幂的性质、运算法则直接求解.
解答 解:$\frac{5}{6}$a${\;}^{\frac{1}{2}}$b${\;}^{-\frac{1}{2}}$×(-3a${\;}^{\frac{1}{6}}$b-1)÷(4a${\;}^{\frac{2}{3}}$b-3)${\;}^{\frac{1}{2}}$
=[$\frac{5}{6}×(-3)÷2$]${a}^{\frac{1}{2}+\frac{1}{6}-\frac{2}{3}×\frac{1}{2}}$${b}^{-\frac{1}{2}-1-(-\frac{3}{2})}$
=-$\frac{5}{4}{a}^{\frac{1}{3}}$.
故答案为:-$\frac{5}{4}{a}^{\frac{1}{3}}$.
点评 本题考查有理数指数幂的化简求值,是基础题,解题时要认真审题,注意有理数数指数幂的性质、运算法则的合理运用.


 出彩同步大试卷系列答案
出彩同步大试卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
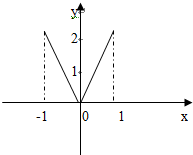
| A. | y=f(|x|) | B. | y=|f(x)| | C. | y=f(-|x|) | D. | y=-f(|x|) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 分组 | 频数 |
| [1.30,1.34) | 4 |
| [1.34,1.38) | 25 |
| [1.38,1.42) | 30 |
| [1.42,1.46) | 29 |
| [1.46,1.50) | 10 |
| [1.50,1.54) | 2 |
| 合计 | 100 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
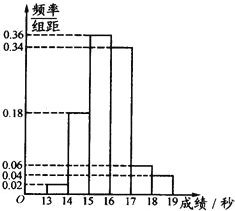 某班50名学生在一次百米测试中,成绩全部介于13秒与19秒之间,如图是测试成绩频率分布直方图.成绩小于17秒的学生人数为( )
某班50名学生在一次百米测试中,成绩全部介于13秒与19秒之间,如图是测试成绩频率分布直方图.成绩小于17秒的学生人数为( )| A. | 45 | B. | 35 | C. | 17 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com