Question

6．随机抽取某高中甲、乙两个班各10名同学，测量他们的身高（单位：cm），获得身高数据的茎叶图如图所示．
（1）甲班和乙班同学身高数据的中位数各是多少？计算甲班的样本方差；
（2）现从乙班这10名同学中随机抽取两名身高不低于173cm的同学，求身高为176cm的同学被抽中的概率．

Answer 1

分析 （1）由中位数和平均数、方差的计算公式，进行计算即可；
（2）利用列举法计算所求的概率值．

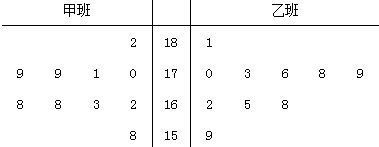
解答 解：（1）根据中位数的定义知，
甲的中位数是：$\frac{170+168}{2}$=169（厘米），
乙的中位数是：$\frac{170+168}{2}$=171.5（厘米）；
根据平均数的公式，计算甲班的平均数为
$\overline{x}$=$\frac{1}{10}$×（158+162+163+168+168+170+170+179+179+182）=170
甲班的样本方差s²=$\frac{1}{10}$×[（150-170）²+（162-170）²+…+（182-170）²]=57.2．
（2）设“身高为176cm的同学被抽中”为事件A．
从乙班10名同学中抽取两名身高不低于173cm的同学有：
（181，173），（181，176），（181，178），（181，179），（179，173），
（179，176），（179，178），（178，173），（178，176），（176，173），
共10个基本事件，而事件A含有4个基本事件：
（181，176），（179，176），（178，176），（176，173）．
所以P（A）=$\frac{4}{10}$=$\frac{2}{5}$．

点评 本题考查了茎叶图的应用问题，也考查了中位数、平均数与方差以及古典概型的计算问题，是基础题目．