
| A. | x2+y2=2 | B. | x2+y2=$\frac{9}{4}$ | C. | x2+y2=4 | D. | x2+y2=9 |
分析 设点P的坐标为(x,y),得到|$\overrightarrow{PO}$|2=x2+y2,结合$\overrightarrow{{P}{A}}$•$\overrightarrow{{P}{B}}$=$\frac{3}{2}$,利用数量积公式展开后再由二倍角的余弦把cos∠APB用P的坐标表示,代入后得答案.
解答 解:设点P的坐标为(x,y),则|$\overrightarrow{PO}$|2=x2+y2,
由$\overrightarrow{{P}{A}}$•$\overrightarrow{{P}{B}}$=$\frac{3}{2}$,得|$\overrightarrow{{P}{A}}$|2cos∠APB=$\frac{3}{2}$,则(|$\overrightarrow{PO}$|2-1)cos∠APB=$\frac{3}{2}$,
设∠APB=2α,则cos∠APB=1-2sin2α=1-2•$\frac{1}{{x}^{2}+{y}^{2}}$,
∴(x2+y2-1)(1-2•$\frac{1}{{x}^{2}+{y}^{2}}$)=$\frac{3}{2}$
整理得:x2+y2=4.
故选:C.
点评 本题主要考查了求轨迹方程的问题,考查了平面向量的数量积运算,考查了数学转化思想方法,属中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x=0 | B. | x=2 | C. | y=2 | D. | y=4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
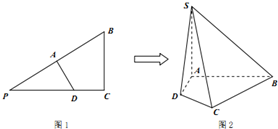 如图1,在△PBC中,∠C=90°,PC=4,BC=3,PD:DC=5:3,AD⊥PB,将△PAD沿AD边折起到SAD位置,如图2,且使SB=$\sqrt{13}$.
如图1,在△PBC中,∠C=90°,PC=4,BC=3,PD:DC=5:3,AD⊥PB,将△PAD沿AD边折起到SAD位置,如图2,且使SB=$\sqrt{13}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x0∈R,f(-x0)≠f(|x0|) | B. | ?x∈R,f(-x)≠f(|x|) | ||
| C. | ?x0∈R,f(-x0)=f(|x0|) | D. | 不存在x0∈R,f(-x0)=f(|x0|) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 组序 | 高度区间 | 频数 | 频率 |
| 1 | [230,235) | 8 | 0.16 |
| 2 | [235,240) | ① | 0.24 |
| 3 | [240,245) | ② | 0.20 |
| 4 | [245,250) | 10 | ③ |
| 5 | [250,255] | 5 | ④ |
| 合计 | 50 | 1.00 | |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(a)>0 | B. | f(a)<0 | ||
| C. | f(a)可以等于0 | D. | f(a)的符号不能确定 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com