Question

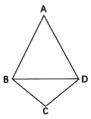
【题目】如图，四边形，，，现将沿折起，当二面角的大小在时，直线和所成角为，则的最大值为（ ）

A. B. C. D.

Answer 1

【答案】C

【解析】

取BD中点O，连结AO，CO，以O为原点，OC为x轴，OD为y轴，过点O作平面BCD的垂线为z轴，建立空间直角坐标系，利用向量法能求出直线AB与CD所成角的余弦值取值范围．

解：取BD中点O，连结AO，CO，

∵AB＝BD＝DA＝4．BC＝CD，∴CO⊥BD，AO⊥BD，且CO＝2，AO，

∴∠AOC是二面角A﹣BD﹣C的平面角，

以O为原点，OC为x轴，OD为y轴，

过点O作平面BCD的垂线为z轴，建立空间直角坐标系，

B（0，﹣2，0），C（2，0，0），D（0，2，0），

设二面角A﹣BD﹣C的平面角为θ，则，

连AO、BO，则∠AOC＝θ，A（），

∴，，

设AB、CD的夹角为α，

则cosα，

∵，∴cos，∴|1|∈[0，1+]．

∴cos的最大值为．

故选：C．