
| A. | 4 | B. | 8 | C. | 16 | D. | 20 |
分析 化简双曲线的标准方程,结合双曲线的定义和余弦定理进行转化求解即可.
解答 解:因为双曲线C:x2-y2=3的标准方程为$\frac{x^2}{3}-\frac{y^2}{3}=1$,
所以$a=\sqrt{3}$,$b=\sqrt{3}$,$c=\sqrt{6}$,
由双曲线的定义和余弦定理得$|{|{P{F_1}}|-|{P{F_2}}|}|=2\sqrt{3}$,${|{P{F_1}}|^2}+{|{P{F_2}}|^2}-2|{P{F_1}}|•|{P{F_2}}|•cos120°=24$,
解得|PF1|•|PF2|=4,${|{P{F_1}}|^2}+{|{P{F_2}}|^2}=20$,
故选:D.
点评 本题主要考查双曲线性质是应用,根据双曲线的定义结合余弦定理是解决本题的关键.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | q1,q3 | B. | q2,q3 | C. | q1,q4 | D. | q2,q4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 今年年初,我国多个地区发生了持续性大规模的雾霾天气,对我们的身体健康产生了巨大的威胁,私家车的尾气排放也是造成雾霾天气的重要因素之一,因此很多城市实施了机动车尾号限行,某报社为了解市区公众对“车辆限行”的态度,随机调查了50人,将调查情况进行整理后制成表:
今年年初,我国多个地区发生了持续性大规模的雾霾天气,对我们的身体健康产生了巨大的威胁,私家车的尾气排放也是造成雾霾天气的重要因素之一,因此很多城市实施了机动车尾号限行,某报社为了解市区公众对“车辆限行”的态度,随机调查了50人,将调查情况进行整理后制成表:| 年龄(岁) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) | [65,75] |
| 调查人数 | 5 | 10 | 15 | 10 | 5 | 5 |
| 赞成人数 | 4 | 6 | 9 | 6 | 3 | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
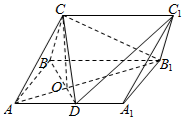 在三棱柱ABC-A1B1C1中,侧面ABB1A1为矩形,AB=$\sqrt{2}$,AA1=2,D为AA1的中点,BD与AB1交于点O,CO⊥侧面ABB1A1.
在三棱柱ABC-A1B1C1中,侧面ABB1A1为矩形,AB=$\sqrt{2}$,AA1=2,D为AA1的中点,BD与AB1交于点O,CO⊥侧面ABB1A1.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 身高(单位:cm) | [180,185) | [185,190) | [190,195) | [195,200) | [200,205) | [205,210] |
| 人数 | 2 | 3 | 3 | 2 | 1 | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com