
分析 由已知及正弦定理可得$\frac{a}{sinA}=\frac{b}{sinB}=\frac{2}{sin60°}=\frac{4\sqrt{3}}{3}$,化简所求即可计算得解.
解答 解:在△ABC中,∵c=2,C=60°,
∴由正弦定理可得:$\frac{a}{sinA}=\frac{b}{sinB}=\frac{2}{sin60°}=\frac{4\sqrt{3}}{3}$,
∴$\frac{a+b}{sinA+sinB}$=$\frac{\frac{4\sqrt{3}}{3}(sinA+sinB)}{sinA+sinB}$=$\frac{{4\sqrt{3}}}{3}$.
故答案为:$\frac{{4\sqrt{3}}}{3}$.
点评 本题主要考查了正弦定理,特殊角的三角函数值在解三角形中的应用,考查了转化思想,属于基础题.


科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 8 | C. | 16 | D. | 20 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
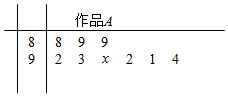 某校开展“向感动中国2015年度人物学习”主题墙报评比,9位评委为A班的墙报,给出的分数如茎叶图所示.记分员在去掉一个最高分和一个最低分后,算得平均分为91,复核员在复核时,发现有一个数字(茎叶图中的x)无法看清,若记分员计算无误,则数字x应该是1.
某校开展“向感动中国2015年度人物学习”主题墙报评比,9位评委为A班的墙报,给出的分数如茎叶图所示.记分员在去掉一个最高分和一个最低分后,算得平均分为91,复核员在复核时,发现有一个数字(茎叶图中的x)无法看清,若记分员计算无误,则数字x应该是1.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,2) | B. | (-2,-1] | C. | (-2,-1) | D. | (2,3) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
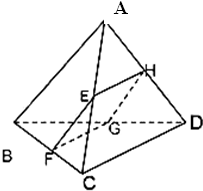 如图,四边形EFGH为空间四边形ABCD的一个截面,若截面为平行四边形,
如图,四边形EFGH为空间四边形ABCD的一个截面,若截面为平行四边形,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com