
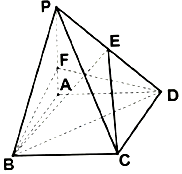
 如图,四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD为菱形,$2\overrightarrow{AF}=\overrightarrow{FP}$,$\overrightarrow{PE}=λ\overrightarrow{ED}$,∠ABC=60°,PA=3,AB=2.
如图,四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD为菱形,$2\overrightarrow{AF}=\overrightarrow{FP}$,$\overrightarrow{PE}=λ\overrightarrow{ED}$,∠ABC=60°,PA=3,AB=2.分析 (1)连结GE,GC,连结AC交BD于O,则GC∥FO,从而GC∥平面BDF,再求出CE∥平面BDF,从而平面BDF∥平面GEC,由此能求出λ.
(2)由题意得FO⊥BD,PO⊥BD,平面BDE与平面BDF所夹角即二面角F-BD-P,其平面角即为∠POF,由此能求出平面BDE与平面BDF所夹角的余弦值.
(3)三棱锥E-BDF的体积${V_{E-BDF}}={V_{B-EDF}}=\frac{1}{3}{V_{B-ADP}}=\frac{1}{3}{V_{P-ADB}}$,由此能求出结果.
解答 解: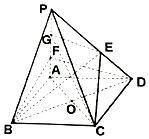 (1)如图,G为PF中点,连结GE,GC,连结AC交BD于O,
(1)如图,G为PF中点,连结GE,GC,连结AC交BD于O,
则GC∥FO,
∵GC?平面BDF,FO?平面BDF,∴GC∥平面BDF,
∵CE与平面BDF没有交点,∴CE∥平面BDF,
∵GC∩CE=C,
∴平面BDF∥平面GEC.
则GE∥FD,故λ=1.
(2)由ABCD为菱形,PA⊥平面ABCD,
由题意得FO⊥BD,PO⊥BD,
而平面BDE与平面BDF所夹角即二面角F-BD-P,
由二面角定义,其平面角即为∠POF,
$cos∠POF=\frac{2+10-4}{{2×\sqrt{2}×\sqrt{10}}}=\frac{{2\sqrt{5}}}{5}$,
∴平面BDE与平面BDF所夹角的余弦值为$\frac{2\sqrt{5}}{5}$.
(3)三棱锥E-BDF的体积:
${V_{E-BDF}}={V_{B-EDF}}=\frac{1}{3}{V_{B-ADP}}=\frac{1}{3}{V_{P-ADB}}=\frac{1}{3}×\frac{1}{3}×\sqrt{3}×3=\frac{{\sqrt{3}}}{3}$.
点评 本题考查线面平行,面面平行的求法应用,考查二面角、柱、锥、台体的体积的求法,考查空间想象能力与计算能力,是中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | $\frac{9}{2}$ | C. | 12 | D. | 27 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0.48 | B. | 0.6 | C. | 0.75 | D. | 0.8 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{4π}{3}$ | B. | 4π | C. | 6π | D. | $\frac{32π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (4,2,2,2) | B. | (9,0,1,0) | C. | (8,0,1,1) | D. | (7,0,1,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com