练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    5．有四人在海边沙滩上发现10颗精致的珍珠，四人约定分配方案：四人先抽签排序①②③④，再由①号提出分配方案，四人表决，至少要有半数的赞成票才算通过，若通过就按此方案分配，否则提出方案的①号淘汰，不再参与分配，接下来由②号提出分配方案，三人表决…，依此类推．假设：1．四人都守信用，愿赌服输；2．提出分配方案的人一定会赞成自己的方案；3．四人都会最大限度争取个人利益．易知若①②都淘汰，则③号的最佳分配方案（能通过且对提出方案者最有利）是（10，0）（表示③、④号分配珍珠数分别是10和0）．问①号的最佳分配方案是（　　）
    A．（4，2，2，2）B．（9，0，1，0）C．（8，0，1，1）D．（7，0，1，2）

    分析 若①②都淘汰，则③号的最佳分配方案（能通过且对提出方案者最有利）是（10，0）（表示③、④号分配珍珠数分别是10和0），可得结论．

    解答 解：根据若①②都淘汰，则③号的最佳分配方案（能通过且对提出方案者最有利）是（10，0）（表示③、④号分配珍珠数分别是10和0），可知①号的最佳分配方案是（9，0，1，0），
    故选B．

    点评 本题考查合情推理，考查学生分析解决问题的能力，属于中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    15．已知圆C1的圆心在坐标原点O，且与直线l1：$x-\sqrt{2}y+6=0$相切，设点A为圆上一动点，AM⊥x轴于点M，且动点N满足$\overrightarrow{ON}=\frac{1}{2}\overrightarrow{OA}+（\frac{{\sqrt{3}}}{3}-\frac{1}{2}）\overrightarrow{OM}$，设动点N的轨迹为曲线C．
    （1）求曲线C的方程；
    （2）若动直线l2：y=kx+m与曲线C有且仅有一个公共点，过F1（-1，0），F2（1，0）两点分别作F1P⊥l2，F2Q⊥l2，垂足分别为P，Q，且记d1为点F1到直线l2的距离，d2为点F2到直线l2的距离，d3为点P到点Q的距离，试探索（d1+d2）•d3是否存在最值？若存在，请求出最值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

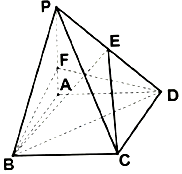    16．如图，四棱锥P-ABCD中，PA⊥平面ABCD，四边形ABCD为菱形，$2\overrightarrow{AF}=\overrightarrow{FP}$，$\overrightarrow{PE}=λ\overrightarrow{ED}$，∠ABC=60°，PA=3，AB=2．
    （1）若直线CE与平面BDF没有公共点，求λ；
    （2）求平面BDE与平面BDF所夹角的余弦值；
    （3）在（1）的条件下，求三棱锥E-BDF的体积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    13．已知数列{an}满足a1=1，an+1=$\frac{a_n}{{{a_n}+2}}（n∈{N^*}）$，则a10=$\frac{1}{1023}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    20．如图，矩形ABCD中，AB=2AD=2，E为边AB的中点，将△ADE沿直线DE翻转成△A1DE，若M为线段A1C的中点，则在△ADE翻转过程中，对于下列说法：
    ①|CA|≥|CA1|
    ②经过点A、E、A1、D的球的体积为2π
    ③一定存在某个位置，使DE⊥A1C
    ④|BM|是定值
    其中正确的说法是①④．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    10．设实数x，y满足约束条件$\left\{\begin{array}{l}{x+y≥0}\\{x-y≤0}\\{x+3y≤3}\end{array}\right.$，则$\frac{x-y}{\sqrt{{x}^{2}+{y}^{2}}}$的取值范围是[$-\sqrt{2}$，-1）∪（-1，0]．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    17．在△ABC中，内角A、B、C所对的边分别是a、b、c，已知A=60°，b=5，c=4．
    （1）求a；
    （2）求sinBsinC的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    14．已知圆C：（x+1）2+y2=12及点F（1，0）点，P在圆上，M，N分别为PF、PC上的点，且满足$\overrightarrow{PM}$=$\overrightarrow{MF}$，$\overrightarrow{MN}$•$\overrightarrow{PF}$=0
    （1）求N的轨迹W的方程；
    （2）是否存在过点F（1，0）的直线l与曲线W相交于A，B两点，并且与曲线W上一点Q，使得四边形OAQB为平行四边形？若存在，求出直线l的方程；若不存在，说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    15．已知变量x，y满足不等式组$\left\{\begin{array}{l}{3x+y-15≤0}\\{x-3y-5≤0}\\{x≥a}\end{array}\right.$使得y≥3x恒成立的实数a的最小值为（　　）
    A．4B．3C．2D．1

    查看答案和解析>>

    同步练习册答案