
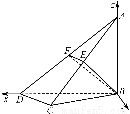
如图甲,在平面四边形ABCD中,已知∠A=45°,∠C=90°,∠ADC=105°,AB=BD,现将四边形ABCD沿BD折起,使平面ABD⊥平面BDC(如图乙),设点E、F分别为棱AC、AD的中点.
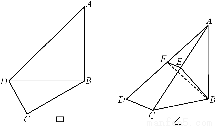
(1)求证:DC⊥平面ABC;
(2)求BF与平面ABC所成角的正弦值;
(3)求二面角B-EF-A的余弦值.
(1)见解析(2)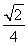 (3)-
(3)-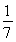
【解析】(1)∵平面ABD⊥平面BDC,又∵AB⊥BD,∴AB⊥平面BDC,故AB⊥DC,又∵∠C=90°,∴DC⊥BC,BC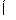 ?ABC平面ABC,DC
?ABC平面ABC,DC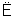 平面ABC,故DC⊥平面ABC.
平面ABC,故DC⊥平面ABC.
(2)如图,以B为坐标原点,BD所在的直线为x轴建立空间直角坐标系如下图示,设CD=a,则BD=AB=2a,BC=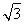 a,AD=2
a,AD=2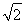 a,可得B(0,0,0),D(2a,0,0),A(0,0,2a),C
a,可得B(0,0,0),D(2a,0,0),A(0,0,2a),C ,F(a,0,a),
,F(a,0,a),
∴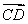 =
= ,
,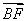 =(a,0,a).
=(a,0,a).
设BF与平面ABC所成的角为θ,由(1)知DC⊥平面ABC,
∴cos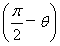 =
=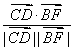 =
= =
=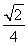 ,∴sinθ=
,∴sinθ=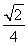 .
.
(3)由(2)知FE⊥平面ABC,又∵BE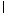 平面ABC,AE
平面ABC,AE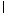 平面ABC,∴FE⊥BE,FE⊥AE,
平面ABC,∴FE⊥BE,FE⊥AE,
∴∠AEB为二面角B-EF-A的平面角.
在△AEB中,AE=BE=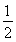 AC=
AC=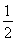
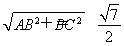 a,
a,
∴cos∠AEB=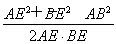 =-
=-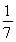 ,即所求二面角B-EF-A的余弦为-
,即所求二面角B-EF-A的余弦为-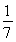 .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第六章第4课时练习卷(解析版) 题型:填空题
若对满足条件x+y+3=xy(x>0,y>0)的任意x、y,(x+y)2-a(x+y)+1≥0恒成立,则实数a的取值范围是________.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第六章第2课时练习卷(解析版) 题型:填空题
已知实数x,y满足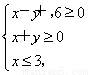 若z=ax+y的最大值为3a+9,最小值为3a-3,则实数a的取值范围为__________.
若z=ax+y的最大值为3a+9,最小值为3a-3,则实数a的取值范围为__________.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第六章第1课时练习卷(解析版) 题型:解答题
某产品生产厂家根据以往的生产销售经验得到下面有关生产销售的统计规律:每生产产品x(百台),总成本为G(x)(万元),其中固定成本为2万元,并且每生产1百台的生产成本为1万元(总成本=固定成本+生产成本);销售收入R(x)(万元)满足:R(x)=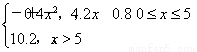 假定该产品产销平衡,那么根据上述统计规律求下列问题.
假定该产品产销平衡,那么根据上述统计规律求下列问题.
(1)要使工厂有赢利,产量x应控制在什么范围内?
(2)工厂生产多少台产品时,可使赢利最多?
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第八章第6课时练习卷(解析版) 题型:解答题
如图所示,四棱锥PABCD中,PA⊥底面ABCD,BC=CD=2,AC=4,∠ACB=∠ACD=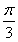 ,F为PC的中点,AF⊥PB.
,F为PC的中点,AF⊥PB.
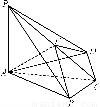
(1)求PA的长;
(2)求二面角B-AF-D的正弦值.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第八章第6课时练习卷(解析版) 题型:解答题
如图所示,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB=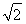 ,AF=1,M是线段EF的中点.
,AF=1,M是线段EF的中点.
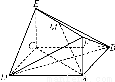
求证:(1)AM∥平面BDE;
(2)AM⊥平面BDF.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第八章第5课时练习卷(解析版) 题型:解答题
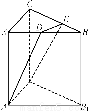
如图,底面边长为a,高为h的正三棱柱ABC-A1B1C1,其中D是AB的中点,E是BC的三等分点.求几何体BDEA1B1C1的体积.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第八章第3课时练习卷(解析版) 题型:解答题
在正方体ABCD-A1B1C1D1中,E、F分别是CD、A1D1中点.
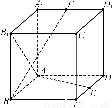
(1)求证:AB1⊥BF;
(2)求证:AE⊥BF;
(3)棱CC1上是否存在点F,使BF⊥平面AEP,若存在,确定点P的位置;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com