
| A. | (1+x)(1+x2)(1+x3)…(1+x11) | |
| B. | (1+x)(1+2x)(1+3x)…(1+11x) | |
| C. | (1+x)(1+2x2)(1+3x3)…(1+11x11) | |
| D. | (1+x)(1+x+x2)(1+x+x2+x3)…(1+x+x2+…+x11) |
分析 x9是由x、x2、x3、x4、x5、x6、x7、x8、x9、x10、x11中的指数和等于9 的那些项的乘积构成,有多少种这样的乘积,就有多少个 x9.各个这样的乘积,分别对应从重量1,2,3,…10,11克的砝码(每种砝码各一个)中,选出若干个表示9克的方法.结合二项式定理及其排列组合的运算性质即可得出.
解答 解:x9是由x、x2、x3、x4、x5、x6、x7、x8、x9、x10、x11中的指数和等于9 的那些项的乘积构成,有多少种这样的乘积,就有多少个 x9.
各个这样的乘积,分别对应从重量1,2,3,…10,11克的砝码(每种砝码各一个)中,选出若干个表示9克的方法.
故“从重量1,2,3,…10,11克的砝码(每种砝码各一个)中选出若干个.
使其总重量恰为9克的方法总数”,
就是“(1+x)(1+x2)(1+x3)…(1+x10)(1+x11)”的展开式中x9的系数”,
故选:A.
点评 本题考查了二项式定理的应用、排列组合的运算性质,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:填空题
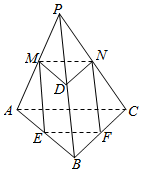
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | 2 | C. | $\sqrt{5}$ | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{3}-1}{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | $\frac{\sqrt{3}+1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{3}+1}}{2}$ | B. | $\frac{{\sqrt{5}+1}}{2}$ | C. | $\sqrt{3}$ | D. | $\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com