
| A. | $\frac{3}{4}$+$\frac{1}{2π}$ | B. | $\frac{1}{2}$+$\frac{1}{π}$ | C. | $\frac{1}{2}$-$\frac{1}{π}$ | D. | $\frac{1}{4}$-$\frac{1}{2π}$ |
分析 由题意易得所求概率为弓形的面积与圆的面积之比,分别求面积可得.
解答 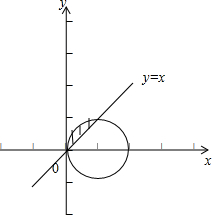 解:∵复数z=(x-1)+yi(x,y∈R)且|z|≤1,
解:∵复数z=(x-1)+yi(x,y∈R)且|z|≤1,
∴|z|=$\sqrt{(x-1)^{2}+{y}^{2}}$≤1,即(x-1)2+y2≤1,
∴点(x,y)在(1,0)为圆心1为半径的圆及其内部,
而y≥x表示直线y=x左上方的部分,(图中阴影弓形)
∴所求概率为弓形的面积与圆的面积之比,
∴所求概率P=$\frac{\frac{1}{4}•π•{1}^{2}-\frac{1}{2}×1×1}{π•{1}^{2}}$=$\frac{1}{4}-\frac{1}{2π}$
故选:D.
点评 本题考查几何概型,涉及复数以及圆的知识,属基础题.


科目:高中数学 来源: 题型:选择题
| A. | (-7,-4) | B. | (7,4) | C. | (-1,4) | D. | (1,4) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 工人编号 | 年龄 | 工人编号 | 年龄 | 工人编号 | 年龄 | 工人编号 | 年龄 |
| 1 2 3 4 5 6 7 8 9 | 40 44 40 41 33 40 45 42 43 | 10 11 12 13 14 15 16 17 18 | 36 31 38 39 43 45 39 38 36 | 19 20 21 22 23 24 25 26 27 | 27 43 41 37 34 42 37 44 42 | 28 29 30 31 32 33 34 35 36 | 34 39 43 38 42 53 37 49 39 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
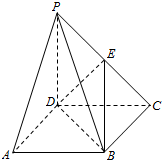 《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的四面体称之为鳖臑.在如图所示的阳马P-ABCD中,侧棱PD⊥底面ABCD,且PD=CD,点E是PC的中点,连接DE、BD、BE.
《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的四面体称之为鳖臑.在如图所示的阳马P-ABCD中,侧棱PD⊥底面ABCD,且PD=CD,点E是PC的中点,连接DE、BD、BE.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com