
分析 (1)利用三角函数恒等变换的应用可求f(x),g(x)解析式,由偶函数的性质可求φ,利用余弦函数的单调性即可得解.
(2)由条件利用函数y=Asin(ωx+φ)的图象变换规律求得函数解析式h(x),由题意可得函数h(x)与y=-k在区间[0,π]上有交点,结合正弦函数的图象可得k的范围.
解答 解:(1)∵f(x)=2$\sqrt{3}$sinx•cosx-2sin2x+1
=$\sqrt{3}$sin2x-(1-cos2x)+1
=2sin(2x+$\frac{π}{6}$),
又∵g(x)=f(x+$\frac{φ}{2}$)=2sin[2(x+$\frac{φ}{2}$)+$\frac{π}{6}$]=2sin(2x+φ+$\frac{π}{6}$)为偶函数,
∴图象关于y轴为对称轴,φ+$\frac{π}{6}$=kπ+$\frac{π}{2}$,k∈Z,
∵φ∈(0,π),
∴φ=$\frac{π}{3}$.…(9分)
则g(x)=2sin(2x+$\frac{π}{2}$)=2cos2x.…(10分)
当cos2x=-1时,函数g(x)取得最大值2,此时x∈{x|x=kπ+$\frac{π}{2}$,k∈Z}.…(12分)
(2)将f(x)的图象向右平移个$\frac{π}{4}$个单位后,得到y=2sin[2(x-$\frac{π}{4}$)+$\frac{π}{6}$]=2sin(2x-$\frac{π}{3}$)的图象,
再将所得图象所有点的横坐标伸长到原来的2倍,纵坐标不变,得到y=2sin(x-$\frac{π}{3}$)的图象.
所以:h(x)=2sin(x-$\frac{π}{3}$).
因为:0≤x≤π,
所以:-$\frac{π}{3}$≤x-$\frac{π}{3}$≤$\frac{2π}{3}$,h(x)=2sin(x-$\frac{π}{3}$)∈[-$\sqrt{3}$,2],
因为:关于x的方程h(x)+k=0,在区间[0,π]上有实数解,
所以:-$\sqrt{3}$≤-k≤2,解得实数k的取值范围为:-2≤k$≤\sqrt{3}$.
点评 本题主要考查由函数y=Asin(ωx+φ)的部分图象求解析式,函数y=Asin(ωx+φ)的图象变换规律,正弦函数的图象,三角函数恒等变换的应用,考查了转化思想和数形结合思想,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
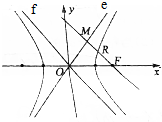 如图,直线e、f为双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)两条渐近线,F为右焦点,过点F作FM∥f,交e于M,交双曲线于R,且$\frac{FR}{FM}$∈[$\frac{1}{2}$,$\frac{2}{3}$],则双曲线的离心率的取值范围是[$\sqrt{2}$,$\sqrt{3}$].
如图,直线e、f为双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)两条渐近线,F为右焦点,过点F作FM∥f,交e于M,交双曲线于R,且$\frac{FR}{FM}$∈[$\frac{1}{2}$,$\frac{2}{3}$],则双曲线的离心率的取值范围是[$\sqrt{2}$,$\sqrt{3}$].查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)在(-∞,0]上单调递减,在(0,+∞)上单调递增 | |
| B. | f(x)在(-∞,0]上单调递增,在(0,+∞)上单调递减 | |
| C. | f(x)在定义域上单调递增 | |
| D. | f(x)在定义域上单调递减 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com