解:(1)设等比数列{a
n}的公比为q,若q=1,则a
n=a
1,a
n+1=a
1,S
n=na
1,这与a
n+1=2S
n+2矛盾,
故q≠1,由a
n+1=2S
n+2得
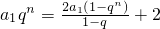
,…(3分)
故取
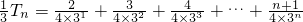
,解得
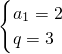
,故a
n=2×3
n-1…(6分)
(2)由(1),知a
n=2×3
n-1,a
n+1=2×3
n因为a
n+1=a
n+(n+1)d
n,所以
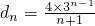
…(8分)
(i)
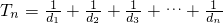
=
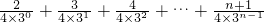
,
则
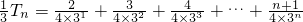
…(10分)
所以
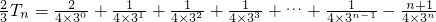
=
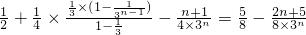
所以
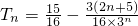
…(12分)
(ii)假设在数列{d
n}中存在d
m,d
k,d
p(其中m,k,p成等差数列)成等比数列
则d
k2=d
md
p,即
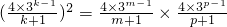
因为m,k,p成等差数列,所以m+p=2k①
上式可以化简为k
2=mp②由①②可得m=k=p这与题设矛盾
所以在数列{d
n}中不存在三项d
m,d
k,d
p(其中m,k,p成等差数列)成等比数列…(16分)
分析:(1)设等比数列{a
n}的公比为q,若q=1,则a
n=a
1,a
n+1=a
1,S
n=na
1,这与a
n+1=2S
n+2矛盾,故q≠1,由a
n+1=2S
n+2得
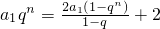
,由此能够推导出a
n=2×3
n-1.
(2)由a
n=2×3
n-1,知a
n+1=2×3
n,因为a
n=a
n+(n+1)d
n,所以
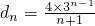
.
(i)
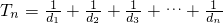
=
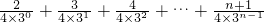
,由错位相减法能够得到
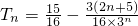
.
(ii)假设在数列{d
n}中存在d
m,d
k,d
p(其中m,k,p成等差数列)成等比数列,则d
k2=d
md
p,由m,k,p成等差数列,知m+p=2k,由此可得m=k=p这与题设矛盾,所以在数列{d
n}中不存在三项d
m,d
k,d
p(其中m,k,p成等差数列)成等比数列.
点评:第(1)题考查数列的通项公式的求法,解题时要注意公比是否等于1;第(2)题考查数列的前n项和的计算和等比数列的综合运用,解题时要注意错位相减法的合理运用.

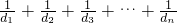 4(n∈N*)5,求Tn;
4(n∈N*)5,求Tn;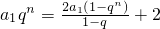 ,…(3分)
,…(3分)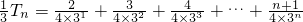 ,解得
,解得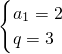 ,故an=2×3n-1…(6分)
,故an=2×3n-1…(6分)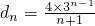 …(8分)
…(8分)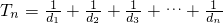 =
=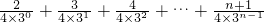 ,
,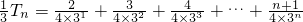 …(10分)
…(10分)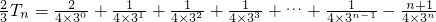
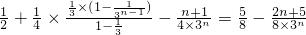
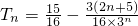 …(12分)
…(12分)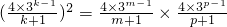
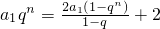 ,由此能够推导出an=2×3n-1.
,由此能够推导出an=2×3n-1.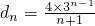 .
.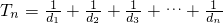 =
=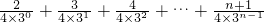 ,由错位相减法能够得到
,由错位相减法能够得到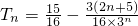 .
.

 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案