
【题目】如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,

(1)证明:PA∥平面EDB
(2)证明:平面BDE![]() 平面PCB
平面PCB
【答案】(1)见解析;(2)见解析
【解析】试题分析:(1)取BD中点O,由三角形中位线性质得OE//PA,再根据线面平行判定定理得结论,(2)先根据等腰三角形性质得DE垂直PC,再根据PD垂直平面ABCD得平面PDC垂直平面ABCD,再根据ABCD是正方形得CD垂直BC,因此由面面垂直性质定理得BC垂直平面PCD,即BC垂直DE,最后根据线面垂直判定定理得DE垂直平面PBC,即得平面BDE![]() 平面PCB.
平面PCB.
试题解析:(1)取BD中点O,则OE//PA,所以PA//平面EDB
(2)由条件得PD垂直EDB,所以PD垂直BC,又CD垂直BC,所以BC垂直PCD,即BC垂直DE,又DE垂直PC,所以DE垂直平面PBC,即平面BDE![]() 平面PCB.
平面PCB.
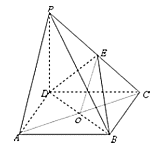
点睛:垂直、平行关系证明中应用转化与化归思想的常见类型.
(1)证明线面、面面平行,需转化为证明线线平行.
(2)证明线面垂直,需转化为证明线线垂直.
(3)证明线线垂直,需转化为证明线面垂直.


 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2+ax+b , g(x)=ex(cx+d),若曲线y=f(x)和曲线y=g(x)都过点P(0,2),且在点P处有相同的切线y=4x+2.
(1)求a , b , c , d的值;
(2)若x≥-2时,恒有f(x)≤kg(x),求k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在2015﹣2016赛季CBA联赛中,某队甲、乙两名球员在前10场比赛中投篮命中情况统计如下表(注:表中分数 ![]() ,N表示投篮次数,n表示命中次数),假设各场比赛相互独立.
,N表示投篮次数,n表示命中次数),假设各场比赛相互独立.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
甲 |
|
|
|
|
|
|
|
|
|
|
乙 |
|
|
|
|
|
|
|
|
|
|
根据统计表的信息:
(1)从上述比赛中等可能随机选择一场,求甲球员在该场比赛中投篮命中率大于0.5的概率;
(2)试估计甲、乙两名运动员在下一场比赛中恰有一人命中率超过0.5的概率;
(3)在接下来的3场比赛中,用X表示这3场比赛中乙球员命中率超过0.5的场次,试写出X的分布列,并求X的数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知长方形 ![]() ,
, ![]() ,
, ![]() ,以
,以 ![]() 的中点
的中点 ![]() 为原点,建立如图所示的平面直角坐标系
为原点,建立如图所示的平面直角坐标系 ![]() .
.
(1)求以 ![]() 为焦点,且过
为焦点,且过 ![]() 两点的椭圆的标准方程;
两点的椭圆的标准方程;
(2)在(1)的条件下,过点 ![]() 作直线
作直线 ![]() 与椭圆交于不同的两点
与椭圆交于不同的两点 ![]() ,设
,设 ![]() ,点
,点 ![]() 坐标为
坐标为 ![]() ,若
,若 ![]() ,求
,求 ![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系中,以坐标原点 ![]() 为极点,
为极点, ![]() 轴的非负半轴为极轴建立极坐标系.已知点
轴的非负半轴为极轴建立极坐标系.已知点 ![]() 的极坐标为
的极坐标为 ![]() ,曲线
,曲线 ![]() 的参数方程为
的参数方程为 ![]() 为参数).
为参数).
(1)直线 ![]() 过
过 ![]() 且与曲线
且与曲线 ![]() 相切,求直线
相切,求直线 ![]() 的极坐标方程;
的极坐标方程;
(2)点 ![]() 与点
与点 ![]() 关于
关于 ![]() 轴对称,求曲线
轴对称,求曲线 ![]() 上的点到点
上的点到点 ![]() 的距离的取值范围.
的距离的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,
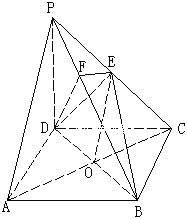
(1)证明:PA∥平面EDB
(2)证明:平面BDE![]() 平面PCB
平面PCB
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在矩形ABCD中,|AB|=4,|AD|=2,O为AB中点,P,Q分别是AD和CD上的点,且满足① ![]() =
= ![]() ,②直线AQ与BP的交点在椭圆E:
,②直线AQ与BP的交点在椭圆E: ![]() +
+ ![]() =1(a>b>0)上.
=1(a>b>0)上.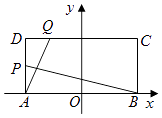
(Ⅰ)求椭圆E的方程;
(Ⅱ)设R为椭圆E的右顶点,M为椭圆E第一象限部分上一点,作MN垂直于y轴,垂足为N,求梯形ORMN面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com