
分析 椭圆C:$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1与函数y=tan$\frac{x}{4}$的图象相交于A1,A2两点,可知:A1,A2两点关于原点对称,设A1(x1,y1),A2(-x1,-y1),P(x0,y0),分别代入椭圆方程可得:${y}_{0}^{2}-{y}_{1}^{2}$=$\frac{3}{4}({x}_{1}^{2}-{x}_{0}^{2})$.由于直线PA2的斜率k1的取值范围[-2,-1],可得-2≤$\frac{{y}_{0}-{y}_{1}}{{x}_{0}-{x}_{1}}$≤-1,${k}_{P{A}_{2}}$=$\frac{{y}_{0}+{y}_{1}}{{x}_{0}+{x}_{1}}$=k2,可得k1k2=$-\frac{3}{4}$.即可得出.
解答 解:∵椭圆C:$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1与函数y=tan$\frac{x}{4}$的图象相交于A1,A2两点,
∴A1,A2两点关于原点对称,设A1(x1,y1),A2(-x1,-y1),$\frac{{x}_{1}^{2}}{4}+\frac{{y}_{1}^{2}}{3}$=1,${y}_{1}^{2}$=$\frac{3}{4}(4-{x}_{1}^{2})$.
设P(x0,y0),则$\frac{{x}_{0}^{2}}{4}+\frac{{y}_{0}^{2}}{3}$=1,可得:${y}_{0}^{2}$=$\frac{3}{4}(4-{x}_{0}^{2})$.
∴${y}_{0}^{2}-{y}_{1}^{2}$=$\frac{3}{4}({x}_{1}^{2}-{x}_{0}^{2})$.
∵直线PA2的斜率k1的取值范围[-2,-1],
∴-2≤$\frac{{y}_{0}+{y}_{1}}{{x}_{0}+{x}_{1}}$≤-1,
${k}_{P{A}_{2}}$=$\frac{{y}_{0}+{y}_{1}}{{x}_{0}+{x}_{1}}$=k2,
∴k1k2=$\frac{{y}_{0}^{2}-{y}_{1}^{2}}{{x}_{0}^{2}-{x}_{1}^{2}}$=$\frac{\frac{3}{4}({x}_{1}^{2}-{x}_{0}^{2})}{{x}_{0}^{2}-{x}_{1}^{2}}$=$-\frac{3}{4}$.
∴${k}_{1}=-\frac{3}{4{k}_{2}}$,
∴$-2≤-\frac{3}{4{k}_{2}}≤$-1,
解得$\frac{3}{8}≤{k}_{2}≤\frac{3}{4}$.
那么直线PA1斜率的取值范围是$[\frac{3}{8},\frac{3}{4}]$.
故答案为:$[\frac{3}{8},\frac{3}{4}]$.
点评 本题考查了椭圆的标准方程及其性质、正切函数的对称性、“点差法”、斜率计算公式、不等式的性质,考查了推理能力与计算能力,属于难题.


科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | 1 | C. | $\frac{{\sqrt{2}}}{2}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{x^2}{16}-\frac{y^2}{9}$=1(x>0) | B. | $\frac{x^2}{16}-\frac{y^2}{9}$=1 | C. | $\frac{x^2}{16}-\frac{y^2}{9}$=1(x<0) | D. | $\frac{x^2}{25}+\frac{y^2}{9}$=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
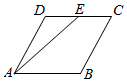
| A. | $\sqrt{7}$ | B. | 5 | C. | $\sqrt{21}$ | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
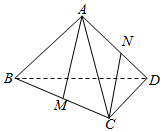 空间四边形ABCD中,AB=BC=CD=DA=AC=BD=a,M,N分别是BC与AD的中点,设AM和CN所成角为α,则cosα的值为( )
空间四边形ABCD中,AB=BC=CD=DA=AC=BD=a,M,N分别是BC与AD的中点,设AM和CN所成角为α,则cosα的值为( )| A. | $\frac{2}{3}$ | B. | $\frac{1}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|x≤0} | B. | {x|x≥2} | C. | {x|x<0或x>2} | D. | {x|x≤0或x≥2} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com