【题目】如图所示的四边形ABCD，已知 
=（6，1）， 
=（x，y）， 
=（﹣2，﹣3）
（1）若 
且﹣2≤x＜1，求函数y=f（x）的值域；
（2）若 且 
，求x，y的值及四边形ABCD的面积．
【答案】
（1）解：∵ 
，
∴ 
．
∵ 
，∴x（2﹣y）﹣y（﹣x﹣4）=0，
∴ 
，∴ 
，
又∵﹣2≤x＜1，∴y∈（﹣ 
，1]，
即函数y=f（x）的值域为 
（2）解：∵ 
，
由 
，可得 
=0，∴（x+6）（x﹣2）+（y+1）（y﹣3）=0，
又 
，由（1）得x+2y=0，联立可得： 
．
若x=﹣6，y=3，则 
=（0，4）， 
=（﹣8，0），∴S四边形ABCD= | || |=16，
若x=2，y=﹣1，则 =（8，0）， =（0，﹣4），∴S四边形ABCD= | || |=16，
综上：四边形ABCD的面积为16．
【解析】（1）由已知运用向量的坐标运算根据两个向量共线得到x、y的函数关系式，由已知条件即可求出函数的值域。（2）根据向量共线以及向量垂直结合（1）可得到关于x、y的方程，再分情况利用对角线垂直的条件求出四边形的面积
学业测评一课一测系列答案科目：高中数学 来源： 题型：
【题目】已知函数
对任意实数
均有
，其中常数
为负数，且
在区间
上有表达式
.
(1)写出
在
上的表达式，并写出函数
在
上的单调区间(不用过程，直接写出即可)；
(2)求出
在
上的最小值与最大值，并求出相应的自变量的取值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某同学参加学校自主招生3门课程的考试，假设该同学第一门课程取得优秀成绩概率为 
，第二、第三门课程取得优秀成绩的概率分别为p，q（p＜q），且不同课程是否取得优秀成绩相互独立，记ξ为该生取得优秀成绩的课程数，其分布列为
ξ | 0 | 1 | 2 | 3 |
p |
| x | y |
|
（Ⅰ）求该生至少有1门课程取得优秀成绩的概率及求p，q的值；
（Ⅱ）求该生取得优秀成绩课程门数的数学期望Eξ．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设函数
，则下列结论正确的是__________．（写出所有正确的编号）①
的最小正周期为
；②
在区间
上单调递增；③
取得最大值的
的集合为
④将
的图像向左平移
个单位，得到一个奇函数的图像
查看答案和解析>>
科目：高中数学 来源： 题型：
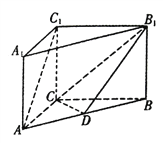
【题目】直三棱柱
中， 
， 
， 
，点
是线段
上的动点.
（1）当点
是
的中点时，求证： 
平面
；
（2）线段
上是否存在点
，使得平面
平面
？若存在，试求出
的长度；若不存在，请说明理由.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】李庄村某社区电费收取有以下两种方案供农户选择：
方案一：每户每月收管理费2元，月用电不超过30度，每度0.4元，超过30度时，超过部分按每度0.5元.
方案二：不收管理费，每度0.48元.
（1）求方案一收费
元与用电量
（度）间的函数关系；
（2）小李家九月份按方案一交费34元，问小李家该月用电多少度？
（3）小李家月用电量在什么范围时，选择方案一比选择方案二更好？
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知椭圆 
： 
的离心率为 
，且过点 
， 
， 
是椭圆 上异于长轴端点的两点.
（1）求椭圆 的方程；
（2）已知直线 
： 
，且 
，垂足为 
， 
，垂足为 
，若 
，且 
的面积是 
面积的5倍，求 面积的最大值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数
为定义在
上的奇函数.
（Ⅰ）求
的解析式；
（Ⅱ）判断
在定义域
上的单调性，并用函数单调性定义给予证明；
（Ⅲ）若关于
的方程
在
上有解，求实数
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
