
【题目】已知函数![]() 为定义在
为定义在![]() 上的奇函数.
上的奇函数.
(Ⅰ)求![]() 的解析式;
的解析式;
(Ⅱ)判断![]() 在定义域
在定义域![]() 上的单调性,并用函数单调性定义给予证明;
上的单调性,并用函数单调性定义给予证明;
(Ⅲ)若关于![]() 的方程
的方程![]() 在
在![]() 上有解,求实数
上有解,求实数![]() 的取值范围.
的取值范围.
科目:高中数学 来源: 题型:
【题目】如图所示的四边形ABCD,已知 ![]() =(6,1),
=(6,1), ![]() =(x,y),
=(x,y), ![]() =(﹣2,﹣3)
=(﹣2,﹣3)
(1)若 ![]() 且﹣2≤x<1,求函数y=f(x)的值域;
且﹣2≤x<1,求函数y=f(x)的值域;
(2)若 ![]() 且
且 ![]() ,求x,y的值及四边形ABCD的面积.
,求x,y的值及四边形ABCD的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sin2x﹣ ![]() sinxcosx+
sinxcosx+ ![]() ,g(x)=mcos(x+
,g(x)=mcos(x+ ![]() )﹣m+2
)﹣m+2
(1)若对任意的x1 , x2∈[0,π],均有f(x1)≥g(x2),求m的取值范围;
(2)若对任意的x∈[0,π],均有f(x)≥g(x),求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 的圆心为
的圆心为![]() ,半径为1,点
,半径为1,点![]() .
.
(Ⅰ)写出圆![]() 的标准方程,并判断点
的标准方程,并判断点![]() 与圆
与圆![]() 的位置关系;
的位置关系;
(Ⅱ)若一条光线从点![]() 射出,经
射出,经![]() 轴反射后,反射光线经过圆心
轴反射后,反射光线经过圆心![]() ,求入射光线所在直线的方程.
,求入射光线所在直线的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某研究所计划利用“神十”宇宙飞船进行新产品搭载实验,计划搭载若干件新产品A、B,该所要根据该产品的研制成本、产品重量、搭载实验费用和预计产生的收益来决定具体搭载安排,有关数据如表:
每件产品A | 每件产品B | ||
研制成本、搭载 | 20 | 30 | 计划最大资金额 |
产品重量(千克) | 10 | 5 | 最大搭载重量110千克 |
预计收益(万元) | 80 | 60 |
分别用x,y表示搭载新产品A,B的件数.总收益用Z表示
(Ⅰ)用x,y列出满足生产条件的数学关系式,并画出相应的平面区域;
(Ⅱ)问分别搭载新产品A、B各多少件,才能使总预计收益达到最大?并求出此最大收益.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知一直线与椭圆4x2+9y2=36相交于A、B两点,弦AB的中点坐标为M(1,1),则直线AB方程为( )
A.4x+9y﹣13=0
B.4x+9y+13=0
C.9x+4y﹣13=0
D.9x+4y+13=0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某学校有一块直角三角形空地![]() ,其中
,其中![]() ,
, ![]() ,
, ![]() ,该校欲在此空地上建造一平行四边形生物实践基地
,该校欲在此空地上建造一平行四边形生物实践基地![]() ,点
,点![]() 分别在
分别在![]() 上.
上.
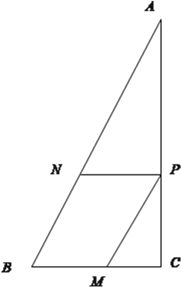
(1)若四边形![]() 为菱形,求基地边
为菱形,求基地边![]() 的长;
的长;
(2)求生物实践基地的最大占地面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如果函数![]() 在其定义域内存在实数
在其定义域内存在实数![]() ,使得
,使得![]() 成立,则称函数
成立,则称函数![]() 为“可拆分函数”.
为“可拆分函数”.
(1)试判断函数![]() 是否为“可拆分函数”?并说明你的理由;
是否为“可拆分函数”?并说明你的理由;
(2)证明:函数![]() 为“可拆分函数”;
为“可拆分函数”;
(3)设函数![]() 为“可拆分函数”,求实数
为“可拆分函数”,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com