
【题目】已知圆![]() 的圆心为
的圆心为![]() ,半径为1,点
,半径为1,点![]() .
.
(Ⅰ)写出圆![]() 的标准方程,并判断点
的标准方程,并判断点![]() 与圆
与圆![]() 的位置关系;
的位置关系;
(Ⅱ)若一条光线从点![]() 射出,经
射出,经![]() 轴反射后,反射光线经过圆心
轴反射后,反射光线经过圆心![]() ,求入射光线所在直线的方程.
,求入射光线所在直线的方程.
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:高中数学 来源: 题型:
【题目】某同学参加学校自主招生3门课程的考试,假设该同学第一门课程取得优秀成绩概率为 ![]() ,第二、第三门课程取得优秀成绩的概率分别为p,q(p<q),且不同课程是否取得优秀成绩相互独立,记ξ为该生取得优秀成绩的课程数,其分布列为
,第二、第三门课程取得优秀成绩的概率分别为p,q(p<q),且不同课程是否取得优秀成绩相互独立,记ξ为该生取得优秀成绩的课程数,其分布列为
ξ | 0 | 1 | 2 | 3 |
p |
| x | y |
|
(Ⅰ)求该生至少有1门课程取得优秀成绩的概率及求p,q的值;
(Ⅱ)求该生取得优秀成绩课程门数的数学期望Eξ.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]() :
: ![]() 的离心率为
的离心率为 ![]() ,且过点
,且过点 ![]() ,
, ![]() ,
, ![]() 是椭圆
是椭圆 ![]() 上异于长轴端点的两点.
上异于长轴端点的两点.
(1)求椭圆 ![]() 的方程;
的方程;
(2)已知直线 ![]() :
: ![]() ,且
,且 ![]() ,垂足为
,垂足为 ![]() ,
, ![]() ,垂足为
,垂足为 ![]() ,若
,若 ![]() ,且
,且 ![]() 的面积是
的面积是 ![]() 面积的5倍,求
面积的5倍,求 ![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设△ABC的内角A,B,C所对的边分别为a,b,c,若三边的长为连续的三个正整数,且A>B>C,3b=20acos A,则sin A:sin B:sin C为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一副直角三角板(如图1)拼接,将△BCD折起,得到三棱锥A﹣BCD(如图2).
(1)若E,F分别为AB,BC的中点,求证:EF∥平面ACD;
(2)若平面ABC⊥平面BCD,求证:平面ABD⊥平面ACD.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下四个关于圆锥曲线的命题中:
①双曲线 ![]() 与椭圆
与椭圆 ![]() 有相同的焦点;
有相同的焦点;
②以抛物线的焦点弦(过焦点的直线截抛物线所得的线段)为直径的圆与抛物线的准线是相切的;
③设A、B为两个定点,k为常数,若|PA|﹣|PB|=k,则动点P的轨迹为双曲线;
④过定圆C上一点A作圆的动弦AB,O为原点,若 ![]() 则动点P的轨迹为椭圆.其中正确的个数是( )
则动点P的轨迹为椭圆.其中正确的个数是( )
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 为定义在
为定义在![]() 上的奇函数.
上的奇函数.
(Ⅰ)求![]() 的解析式;
的解析式;
(Ⅱ)判断![]() 在定义域
在定义域![]() 上的单调性,并用函数单调性定义给予证明;
上的单调性,并用函数单调性定义给予证明;
(Ⅲ)若关于![]() 的方程
的方程![]() 在
在![]() 上有解,求实数
上有解,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某个体服装店经营某种服装,在某周内获得的纯利润y(单位:元)与该周每天销售这种服装的件数x之间的一组数据关系如下表:
x | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
y | 66 | 69 | 73 | 81 | 89 | 90 | 91 |
(1)求纯利润y与每天销售件数x之间的回归方程;
(2)若该周内某天销售服装20件,估计可获得纯利润多少元?
已知:![]() =280,
=280,![]() xiyi=3 487,
xiyi=3 487,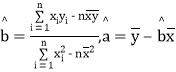 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com