
【题目】一副直角三角板(如图1)拼接,将△BCD折起,得到三棱锥A﹣BCD(如图2).
(1)若E,F分别为AB,BC的中点,求证:EF∥平面ACD;
(2)若平面ABC⊥平面BCD,求证:平面ABD⊥平面ACD.
【答案】
(1)证明:因为E,F分别为AB,BC的中点,所以EF∥AC.
又EF平面ACD,AC平面ACD,所以EF∥平面ACD.
(2)因为平面ABC⊥平面BCD,平面ABC∩平面BCD=BC,
CD平面BCD,CD⊥BC,所以CD⊥平面ABC.
因为AB平面ABC,所以CD⊥AB.
又因为AB⊥AC,AC∩CD=C,AC平面ACD,CD平面ACD,
所以AB⊥平面ACD.
又AB平面ABD,所以平面ABD⊥平面ACD.
【解析】(1)根据中位线性质可得EF∥AC,由线面平行相关性质可得EF∥平面ACD,(2)由平面ABC⊥平面BCD,CD⊥BC,所以CD⊥平面ABC,从而得到CD⊥AB,结合AB⊥AC,可得出AB⊥平面ACD,即平面ABD⊥平面ACD.
【考点精析】本题主要考查了直线与平面平行的判定和平面与平面垂直的判定的相关知识点,需要掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行;一个平面过另一个平面的垂线,则这两个平面垂直才能正确解答此题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】某工厂某种产品的年固定成本为250万元,每生产![]() 件,需另投入成本
件,需另投入成本![]() ,当年产量不足80件时,
,当年产量不足80件时, ![]() (万元),当年产量不少于80件时
(万元),当年产量不少于80件时![]() (万元),每件商品售价50万元,通过市场分析,该厂生产的商品能全部售完.
(万元),每件商品售价50万元,通过市场分析,该厂生产的商品能全部售完.
(1)写出年利润![]() (万元)关于年产量
(万元)关于年产量![]() (件)的函数解析式;
(件)的函数解析式;
(2)年产量为多少件时,该厂在这一商品的生产中所获利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某车间的一台机床生产出一批零件,现从中抽取8件,将其编为![]() ,
, ![]() ,…,
,…, ![]() ,测量其长度(单位:
,测量其长度(单位: ![]() ),得到下表中数据:
),得到下表中数据:
编号 |
|
|
|
|
|
|
|
|
长度 | 1.49 | 1.46 | 1.51 | 1.51 | 1.53 | 1.51 | 1.47 | 1.51 |
其中长度在区间![]() 内的零件为一等品.
内的零件为一等品.
(1)从上述8个零件中,随机抽取一个,求这个零件为一等品的概率;
(2)从一等品零件中,随机抽取2个.
①用零件的编号列出所有可能的抽取结果;
②求这2个零件长度相等的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sin2x﹣ ![]() sinxcosx+
sinxcosx+ ![]() ,g(x)=mcos(x+
,g(x)=mcos(x+ ![]() )﹣m+2
)﹣m+2
(1)若对任意的x1 , x2∈[0,π],均有f(x1)≥g(x2),求m的取值范围;
(2)若对任意的x∈[0,π],均有f(x)≥g(x),求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设a,b∈R,c∈[0,2π),若对于任意实数x都有2sin(3x﹣ ![]() )=asin(bx+c),则满足条件的有序实数组(a,b,c)的组数为 .
)=asin(bx+c),则满足条件的有序实数组(a,b,c)的组数为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 的圆心为
的圆心为![]() ,半径为1,点
,半径为1,点![]() .
.
(Ⅰ)写出圆![]() 的标准方程,并判断点
的标准方程,并判断点![]() 与圆
与圆![]() 的位置关系;
的位置关系;
(Ⅱ)若一条光线从点![]() 射出,经
射出,经![]() 轴反射后,反射光线经过圆心
轴反射后,反射光线经过圆心![]() ,求入射光线所在直线的方程.
,求入射光线所在直线的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某研究所计划利用“神十”宇宙飞船进行新产品搭载实验,计划搭载若干件新产品A、B,该所要根据该产品的研制成本、产品重量、搭载实验费用和预计产生的收益来决定具体搭载安排,有关数据如表:
每件产品A | 每件产品B | ||
研制成本、搭载 | 20 | 30 | 计划最大资金额 |
产品重量(千克) | 10 | 5 | 最大搭载重量110千克 |
预计收益(万元) | 80 | 60 |
分别用x,y表示搭载新产品A,B的件数.总收益用Z表示
(Ⅰ)用x,y列出满足生产条件的数学关系式,并画出相应的平面区域;
(Ⅱ)问分别搭载新产品A、B各多少件,才能使总预计收益达到最大?并求出此最大收益.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某学校有一块直角三角形空地![]() ,其中
,其中![]() ,
, ![]() ,
, ![]() ,该校欲在此空地上建造一平行四边形生物实践基地
,该校欲在此空地上建造一平行四边形生物实践基地![]() ,点
,点![]() 分别在
分别在![]() 上.
上.
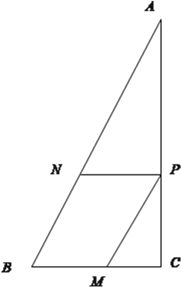
(1)若四边形![]() 为菱形,求基地边
为菱形,求基地边![]() 的长;
的长;
(2)求生物实践基地的最大占地面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com