【题目】如图，某学校有一块直角三角形空地
，其中
， 
， 
，该校欲在此空地上建造一平行四边形生物实践基地
，点
分别在
上.
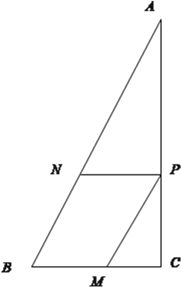
（1）若四边形
为菱形，求基地边
的长；
（2）求生物实践基地的最大占地面积.
科目：高中数学 来源： 题型：
【题目】李庄村某社区电费收取有以下两种方案供农户选择：
方案一：每户每月收管理费2元，月用电不超过30度，每度0.4元，超过30度时，超过部分按每度0.5元.
方案二：不收管理费，每度0.48元.
（1）求方案一收费
元与用电量
（度）间的函数关系；
（2）小李家九月份按方案一交费34元，问小李家该月用电多少度？
（3）小李家月用电量在什么范围时，选择方案一比选择方案二更好？
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】一副直角三角板（如图1）拼接，将△BCD折起，得到三棱锥A﹣BCD（如图2）．
（1）若E，F分别为AB，BC的中点，求证：EF∥平面ACD；
（2）若平面ABC⊥平面BCD，求证：平面ABD⊥平面ACD．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数
为定义在
上的奇函数.
（Ⅰ）求
的解析式；
（Ⅱ）判断
在定义域
上的单调性，并用函数单调性定义给予证明；
（Ⅲ）若关于
的方程
在
上有解，求实数
的取值范围.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某个体服装店经营某种服装,在某周内获得的纯利润y(单位:元)与该周每天销售这种服装的件数x之间的一组数据关系如下表:
x | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
y | 66 | 69 | 73 | 81 | 89 | 90 | 91 |
(1)求纯利润y与每天销售件数x之间的回归方程;
(2)若该周内某天销售服装20件,估计可获得纯利润多少元?
已知:
=280,
xiyi=3 487,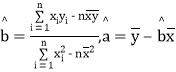
.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】过三点A（﹣3，2），B（3，﹣6），C（0，3）的圆的方程为（ ）
A.x2+y2+4y﹣21=0
B.x2+y2﹣4y﹣21=0
C.x2+y2+4y﹣96=0
D.x2+y2﹣4y﹣96=0
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】统计表明，家庭的月理财投入
（单位：千元）与月收入
（单位：千元）之间具有线性相关关系．某银行随机抽取5个家庭，获得第
（
1，2，3，4，5）个家庭的月理财投入
与月收入
的数据资料，经计算得
，
，
，
．
（1）求关于的回归方程
；
（2）判断与之间是正相关还是负相关；
（3）若某家庭月理财投入为5千元，预测该家庭的月收入．
附：回归方程的斜率与截距的最小二乘估计公式分别为：
，
，其中
，
为样本平均值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f（x）=m6x﹣4x ， m∈R．
（1）当m= 
时，求满足f（x+1）＞f（x）的实数x的范围；
（2）若f（x）≤9x对任意的x∈R恒成立，求实数m的范围．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
