
【题目】过三点A(﹣3,2),B(3,﹣6),C(0,3)的圆的方程为( )
A.x2+y2+4y﹣21=0
B.x2+y2﹣4y﹣21=0
C.x2+y2+4y﹣96=0
D.x2+y2﹣4y﹣96=0
【答案】A
【解析】解:AB的中点坐标为(0,﹣2),直线AB的斜率为 ![]() ,所以垂直平分线的斜率为
,所以垂直平分线的斜率为 ![]()
则线段AB的垂直平分线方程为y+2= ![]() x,化简得3x﹣4y﹣8=0①;
x,化简得3x﹣4y﹣8=0①;
同理得到AC的中点坐标为( ![]() ,
, ![]() ),直线AC的斜率为
),直线AC的斜率为 ![]() ,所以垂直平分线的斜率为﹣3
,所以垂直平分线的斜率为﹣3
则线段AC的垂直平分线方程为y﹣ ![]() =﹣3(x+
=﹣3(x+ ![]() )化简得6x+2y+4=0②.
)化简得6x+2y+4=0②.
联立①②解得x=0,y=﹣2,则圆心坐标为(0,﹣2),圆的半径r=5
则圆的标准方程为:x2+(y+2)2=25,即x2+y2+4y﹣21=0,
所以答案是:A.
【考点精析】解答此题的关键在于理解圆的一般方程的相关知识,掌握圆的一般方程的特点:(1)①x2和y2的系数相同,不等于0.②没有xy这样的二次项;(2)圆的一般方程中有三个特定的系数D、E、F,因之只要求出这三个系数,圆的方程就确定了;(3)、与圆的标准方程相比较,它是一种特殊的二元二次方程,代数特征明显,圆的标准方程则指出了圆心坐标与半径大小,几何特征较明显.


科目:高中数学 来源: 题型:
【题目】某车间的一台机床生产出一批零件,现从中抽取8件,将其编为![]() ,
, ![]() ,…,
,…, ![]() ,测量其长度(单位:
,测量其长度(单位: ![]() ),得到下表中数据:
),得到下表中数据:
编号 |
|
|
|
|
|
|
|
|
长度 | 1.49 | 1.46 | 1.51 | 1.51 | 1.53 | 1.51 | 1.47 | 1.51 |
其中长度在区间![]() 内的零件为一等品.
内的零件为一等品.
(1)从上述8个零件中,随机抽取一个,求这个零件为一等品的概率;
(2)从一等品零件中,随机抽取2个.
①用零件的编号列出所有可能的抽取结果;
②求这2个零件长度相等的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某研究所计划利用“神十”宇宙飞船进行新产品搭载实验,计划搭载若干件新产品A、B,该所要根据该产品的研制成本、产品重量、搭载实验费用和预计产生的收益来决定具体搭载安排,有关数据如表:
每件产品A | 每件产品B | ||
研制成本、搭载 | 20 | 30 | 计划最大资金额 |
产品重量(千克) | 10 | 5 | 最大搭载重量110千克 |
预计收益(万元) | 80 | 60 |
分别用x,y表示搭载新产品A,B的件数.总收益用Z表示
(Ⅰ)用x,y列出满足生产条件的数学关系式,并画出相应的平面区域;
(Ⅱ)问分别搭载新产品A、B各多少件,才能使总预计收益达到最大?并求出此最大收益.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某学校有一块直角三角形空地![]() ,其中
,其中![]() ,
, ![]() ,
, ![]() ,该校欲在此空地上建造一平行四边形生物实践基地
,该校欲在此空地上建造一平行四边形生物实践基地![]() ,点
,点![]() 分别在
分别在![]() 上.
上.
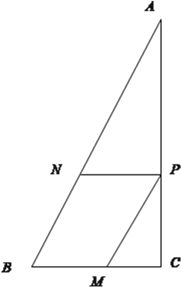
(1)若四边形![]() 为菱形,求基地边
为菱形,求基地边![]() 的长;
的长;
(2)求生物实践基地的最大占地面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】1994年到2016年所有关于某项研究成果的540篇论文分布如下图所示.
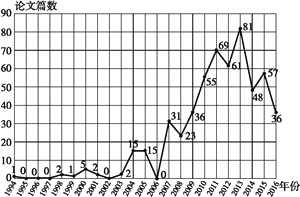
(1)从这540篇论文中随机抽取一篇来研究,那么抽到2016年发表论文的概率是多少?
(2)如果每年发表该领域有国际影响力的论文超过50篇,我们称这一年是该领域的论文“丰年”.若从1994年到2016年中随机抽取连续的两年来研究,那么连续的两年中至少有一年是“丰年”的概率是多少?
(3)由图判断,从哪年开始连续三年论文数量方差最大?(结论不要求证明)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在长方体ABCD﹣A1B1C1D1中,A1C1与B1D1的交点为O1 , AC与BD的交点为O.
(1)求证:直线OO1∥平面BCC1B1;
(2)若AB=BC,求证:直线BO⊥平面ACC1A1 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若存在两个正实数m、n,使得等式a(lnn﹣lnm)(4em﹣2n)=3m成立(其中e为自然对数的底数),则实数a的取值范围是( )
A.(﹣∞,0)
B.(0, ![]() ]
]
C.[ ![]() ,+∞)
,+∞)
D.(﹣∞,0)∪[ ![]() ,+∞)
,+∞)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com