
【题目】设函数![]()
![]() .
.
(Ⅰ)求![]() 的单调区间;
的单调区间;
(Ⅱ)当![]() 时,试判断
时,试判断![]() 零点的个数;
零点的个数;
(Ⅲ)当![]() 时,若对
时,若对![]() ,都有
,都有![]() (
(![]() )成立,求
)成立,求![]() 的最大值.
的最大值.
【答案】(1)当![]() 时,
时,![]() 的单减区间为
的单减区间为![]() ;当
;当![]() 时,
时,![]() 的单减区间为
的单减区间为![]() ,单增区间为
,单增区间为![]() ;(2)两个;(3)0.
;(2)两个;(3)0.
【解析】
(1)求出![]() ,分两种情况讨论
,分两种情况讨论![]() 的范围,在定义域内,分别令
的范围,在定义域内,分别令![]() 求得
求得![]() 的范围,可得函数
的范围,可得函数![]() 增区间,
增区间,![]() 求得
求得![]() 的范围,可得函数
的范围,可得函数![]() 的减区间;(2)当
的减区间;(2)当![]() 时,由(1)可知,
时,由(1)可知,![]() 在
在![]() 是单减函数,在
是单减函数,在![]() 是单增函数,由
是单增函数,由![]() ,
,![]() ,利用零点存在定理可得结果;(3)当
,利用零点存在定理可得结果;(3)当![]() ,
,![]() 为整数,且当
为整数,且当![]() 时,
时,![]() 恒成立,
恒成立,![]() ,利用导数求出
,利用导数求出![]() 的取值范围,从而可得结果.
的取值范围,从而可得结果.
(1)![]() ,
,
![]()
![]() .
.
当![]() 时,
时,![]() 在
在![]() 恒成立,
恒成立,
![]() 在
在![]() 是单减函数.
是单减函数.
当![]() 时,令
时,令![]() ,解之得
,解之得![]() .
.
从而,当![]() 变化时,
变化时,![]() ,
,![]() 随
随![]() 的变化情况如下表:
的变化情况如下表:
| | | |
| - | 0 | + |
| 单调递减 | 单调递增 |
由上表中可知,![]() 在
在![]() 是单减函数,在
是单减函数,在![]() 是单增函数.
是单增函数.
综上,当![]() 时,
时,![]() 的单减区间为
的单减区间为![]() ;
;
当![]() 时,
时,![]() 的单减区间为
的单减区间为![]() ,单增区间为
,单增区间为![]() .
.
(2)当![]() 时,由(1)可知,
时,由(1)可知,![]() 在
在![]() 是单减函数,在
是单减函数,在![]() 是单增函数;
是单增函数;
又![]() ,
,![]() ,
,![]() .
.
![]()
![]() ,
,![]() ;
;
故![]() 在
在![]() 有两个零点.
有两个零点.
(3)当![]() ,
,![]() 为整数,且当
为整数,且当![]() 时,
时,![]() 恒成立
恒成立
![]() .
.
令![]() ,只需
,只需![]() ;
;
又![]() ,
,
由(2)知,![]() 在
在![]() 有且仅有一个实数根
有且仅有一个实数根![]() ,
,
![]() 在
在![]() 上单减,在
上单减,在![]() 上单增;
上单增;
![]()
![]()
又![]() ,
,![]() ,
,
![]()
![]() ,
,![]()
![]() 且
且![]() ,
,
即![]() 代入
代入![]() 式,得
式,得
![]() .
.
而![]() 在
在![]() 为增函数,
为增函数,![]()
![]() ,
,
即![]() .
.
而![]() ,
,![]()
![]() ,
,
![]() 即所求
即所求![]() 的最大值为0.
的最大值为0.


科目:高中数学 来源: 题型:
【题目】某市统计局就某地居民的月收入调查了10000人,并根据所得数据画出样本的频率分布直方图(每个分组包括左端点,不包括右端点,如第一组表示收入在![]() ).
).
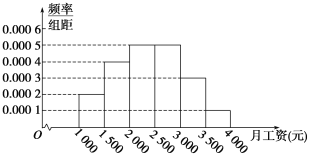
(1)求居民收入在![]() 的频率;
的频率;
(2)根据频率分布直方图算出样本数据的中位数;
(3)为了分析居民的收入与年龄、职业等方面的关系,必须按月收入再从这10000人中按分层抽样方法抽出100人作进一步分析,则月收入在![]() 的这段应抽取多少人?
的这段应抽取多少人?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市通过抽样调查的方法获得了100户居民某月用水量(单位:t)的频率分布直方图:
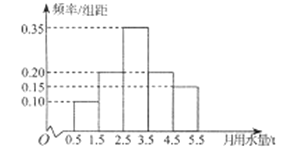
(Ⅰ)求这100户居民该月用水量的平均值;
(Ⅱ)从该月用水量在![]() 和
和![]() 两个区间的用户中,用分层抽样的方法邀请5户的户主共5人参加水价调整方案听证会,现从这5人中随机选取2人在会上进行陈述发言,求选取的2人均来自用水量低于2.5t的用户的概率.
两个区间的用户中,用分层抽样的方法邀请5户的户主共5人参加水价调整方案听证会,现从这5人中随机选取2人在会上进行陈述发言,求选取的2人均来自用水量低于2.5t的用户的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)=asin2x+bcos2x(a,b∈R,ab≠0),若f(x)![]() 对一切x∈R恒成立,给出以下结论:
对一切x∈R恒成立,给出以下结论:
①![]() ;
;
②![]() ;
;
③f(x)的单调递增区间是![]() ;
;
④函数y=f(x)既不是奇函数也不是偶函数;
⑤存在经过点(a,b)的直线与函数f(x)的图象不相交,其中正确结论为_____
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四校锥P﹣ABCD中,底面ABCD是菱形,∠BAD=60°,边长为4的正△PAD所在平面与平面ABCD垂直,点E是AD的中点,点Q是侧棱PC的中点.

(1)求四棱锥P﹣ABCD的体积;
(2)求证:PA∥平面BDQ;
(3)在线段AB上是否存在点F,使直线PF与平面PAD所成的角为30°?若存在,求出AF的长,若不存在,请说明理由?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从全校参加数学竞赛的学生的试卷中,抽取一个样本,考察竞赛的成绩分布,将样本分成![]() 组,绘成频率分布直方图,图中从左到右各小组的长方形的高之比为
组,绘成频率分布直方图,图中从左到右各小组的长方形的高之比为![]() ,最右边一组的频数是
,最右边一组的频数是![]() .
.
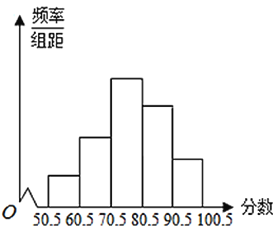
(1)成绩落在哪个范围的人数最多?并求出该小组的频数、频率;
(2)估计这次竞赛中,成绩高于![]() 分的学生占总人数的百分百.
分的学生占总人数的百分百.
查看答案和解析>>
科目:高中数学 来源: 题型:
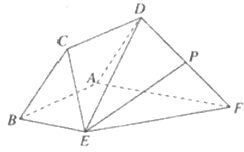
【题目】如图,已知菱形![]() 与直角梯形
与直角梯形![]() 所在的平面互相垂直,其中
所在的平面互相垂直,其中![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 的中点
的中点
(Ⅰ)求证:![]() ;
;
(Ⅱ)求二面角![]() 的余弦值;
的余弦值;
(Ⅲ)设![]() 为线段
为线段![]() 上一点,
上一点,![]() ,若直线
,若直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
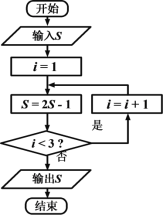
【题目】《算法统宗》是中国古代数学名著,由明代数学家程大位所著,该作完善了珠算口诀,确立了算盘用法,完成了由筹算到珠算的彻底转变,该作中有题为“李白沽酒”“李白街上走,提壶去买酒。遇店加一倍,见花喝一斗,三遇店和花,喝光壶中酒。借问此壶中,原有多少酒?”,如图为该问题的程序框图,若输出的![]() 值为0,则开始输入的
值为0,则开始输入的![]() 值为( )
值为( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
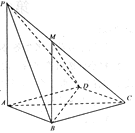
【题目】如图,在四棱锥![]() 中,
中,![]() 平面
平面![]() ,底面
,底面![]() 是菱形,
是菱形,![]() ,
,![]() .
.
(Ⅰ)求证:直线![]() 平面
平面![]() ;
;
(Ⅱ)求直线![]() 与平面
与平面![]() 所成角的正切值;
所成角的正切值;
(Ⅲ)设点![]() 在线段
在线段![]() 上,且二面角
上,且二面角![]() 的余弦值为
的余弦值为![]() ,求点
,求点![]() 到底面
到底面![]() 的距离.
的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com