
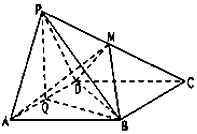
 如图,在四棱锥P-ABCD中,底面ABCD为菱形,其中PA=PD=AD=2,∠BAD=60°,Q为AD的中点.
如图,在四棱锥P-ABCD中,底面ABCD为菱形,其中PA=PD=AD=2,∠BAD=60°,Q为AD的中点.分析 (1)根据三线合一可得AD⊥PQ,AD⊥BQ,故而AD⊥平面PQB;
(2)取PB的中点N,连接MN,AN,QN,则∠BQN为二面角的平面角,根据△PBQ是等腰直角三角形得出∠BQN的大小.
解答  证明:(1)连DB,
证明:(1)连DB,
∵PA=PD,Q为中点,∴AD⊥PQ
在△ADB中,AD=AB,∠BAD=60°,
∴△ABD为等边三角形,又Q为AD的中点,
∴AD⊥BQ,
又PQ∩BQ=Q,PQ?平面PQB,BQ?平面PQB,
∴AD⊥平面PQB.
解:(2)取PB的中点N,连接MN,AN,QN,
则MN∥BC∥AD,
∴MN?平面MAD,
由(1)可知AD⊥平面PBQ,QN?平面PBQ,
∴AD⊥QN,又AD⊥QB,
∴∠NQB是二面角M-AD-B的平面角,
∵平面PAD⊥平面ABCD,∴PQ⊥平面ABD,
∴PQ⊥QB,又△ADP和△ABD是边长为2的等边三角形,
∴PQ=BQ,∠PBQ=45°,
∵N是PB的中点,∴QN=$\frac{1}{2}$PB=BN,
∴∠NQB=∠NBQ=45°.
即二面角M-AD-B的平面角为45°.
点评 本题考查了线面垂直的判定,空间角的计算,作出二面角的平面角是解题关键,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | $-\frac{3}{5}$ | B. | $\frac{3}{5}$ | C. | $-\frac{4}{5}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 17 | C. | 28 | D. | 41 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 对任意的正数M,存在x∈(0,1),使f(x)≥M | |
| B. | 存在正数M,对任意的x∈(0,1),使f(x)≤M | |
| C. | 对任意的x1,x2∈(0,1)且x1<x2,有f(x1)<f(x2) | |
| D. | 对任意的x1,x2∈(0,1)且x1<x2,有f(x1)>f(x2) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [0,2] | B. | (1,2] | C. | [1,2) | D. | (1,4] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 轿车A | 轿车B | 轿车C | |
| 舒适型 | 100 | 150 | z |
| 标准型 | 300 | 450 | 600 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com