
分析 (1)运用代入计算,可得{an}的前3项,猜想an=6n-2,n∈N*;
(2)运用数学归纳法证明,验证n=1时,结论成立;假设n=k,k∈N+时,猜想成立,即有ak=6k-2,再证n=k+1时,结论也成立,注意运用已知条件和假设,化简整理即可得证.
解答 解:(1)由an+5an+1=36n+18,n∈N*,且a1=4,
可得a1+5a2=36+18=54,
即有a2=10,
由a2+5a3=72+18=90,
可得a3=16,
猜想an=6n-2,n∈N*;
(2)证明:①当n=1时,a1=4=6×1-2成立;
②假设n=k,k∈N+时,猜想成立,即有ak=6k-2,
由ak+5ak+1=36k+18,及ak=6k-2,
即5ak+1=36k+18-6k+2=30k+20,
得ak+1=6k+4=6(k+1)-2,即当n=k+1时猜想成立,
由①②可知,an=6n-2对一切正整数n均成立.
点评 本题考查数列的通项公式的求法,注意运用归纳猜想和数学归纳法的证明,由n=k+1运用n=k的假设是证明的关键,考查运算能力,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 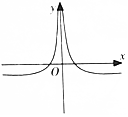 | B. | 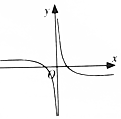 | C. | 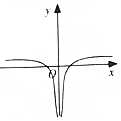 | D. | 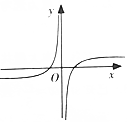 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({-∞,-\frac{8}{5}}]∪[{3,+∞})$ | B. | $[{-1,\frac{1}{7}}]$ | C. | (-1,0]∪[3,+∞) | D. | (-∞,-1]∪[7,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=$\sqrt{x}$ | B. | f(x)=2x | C. | f(x)=sinx | D. | f(x)=arctanx |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
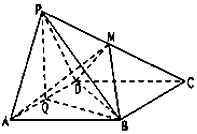 如图,在四棱锥P-ABCD中,底面ABCD为菱形,其中PA=PD=AD=2,∠BAD=60°,Q为AD的中点.
如图,在四棱锥P-ABCD中,底面ABCD为菱形,其中PA=PD=AD=2,∠BAD=60°,Q为AD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | -1 | C. | ±1 | D. | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com