
| A. | 对任意的正数M,存在x∈(0,1),使f(x)≥M | |
| B. | 存在正数M,对任意的x∈(0,1),使f(x)≤M | |
| C. | 对任意的x1,x2∈(0,1)且x1<x2,有f(x1)<f(x2) | |
| D. | 对任意的x1,x2∈(0,1)且x1<x2,有f(x1)>f(x2) |
分析 当x∈(0,1)时,对勾函数y=x+$\frac{1}{x}$为单调减函数,可知t(x)=$\frac{2x}{1+{x}^{2}}$=$\frac{2}{\frac{1}{x}+x}$在区间(0,1)上单调递增,令0<x1<x2<1,则t(x1)<t(x2),∵x∈(0,1),有f($\frac{2x}{1+{x}^{2}}$)=2f(x),
故当x→0+时,有f(0+)=2f(0+),故f(0+)=0,故不存在对任意的正数M,存在x∈(0,1),使f(x)≥M,对于函数f(x)的单调性不能确定.
解答 解:当x∈(0,1)时,对勾函数y=x+$\frac{1}{x}$为单调减函数,
所以t(x)=$\frac{2x}{1+{x}^{2}}$=$\frac{2}{\frac{1}{x}+x}$在区间(0,1)上单调递增,
令0<x1<x2<1,则t(x1)<t(x2),
∵x∈(0,1),有f($\frac{2x}{1+{x}^{2}}$)=2f(x),
∴当x→0+时,有f(0+)=2f(0+),故f(0+)=0,
故不存在对任意的正数M,存在x∈(0,1),使f(x)≥M
对于函数f(x)的单调性不能确定,
故选:B
点评 本题考查了函数的性质,需要对函数的特征进行分析,从而作出判定,属于难题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 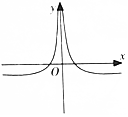 | B. | 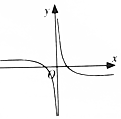 | C. | 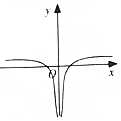 | D. | 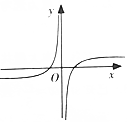 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=$\sqrt{x}$ | B. | f(x)=2x | C. | f(x)=sinx | D. | f(x)=arctanx |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
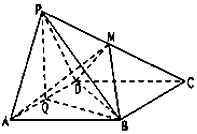 如图,在四棱锥P-ABCD中,底面ABCD为菱形,其中PA=PD=AD=2,∠BAD=60°,Q为AD的中点.
如图,在四棱锥P-ABCD中,底面ABCD为菱形,其中PA=PD=AD=2,∠BAD=60°,Q为AD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图所示的几何体ABCDE,EA⊥平面ABC,EA∥DC,AB⊥AC,EA=AB=AC=2DC,M是线段BD上的动点.
如图所示的几何体ABCDE,EA⊥平面ABC,EA∥DC,AB⊥AC,EA=AB=AC=2DC,M是线段BD上的动点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com