
 如图所示的几何体ABCDE,EA⊥平面ABC,EA∥DC,AB⊥AC,EA=AB=AC=2DC,M是线段BD上的动点.
如图所示的几何体ABCDE,EA⊥平面ABC,EA∥DC,AB⊥AC,EA=AB=AC=2DC,M是线段BD上的动点.分析 (Ⅰ)建立坐标系,求出$\overrightarrow{BC}$,$\overrightarrow{AE},\overrightarrow{AM}$的坐标,利用数量积证明BC⊥AE,BC⊥AM即可得出结论;
(II)求出平面AMC的法向量$\overrightarrow{n}$,设$\overrightarrow{BM}=λ\overrightarrow{AD}$,令|cos<$\overrightarrow{n},\overrightarrow{BD}$>|=sin60°,解出λ即可确定M的位置.
解答 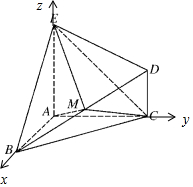 解:(Ⅰ)证明:∵EA⊥平面ABC,AB⊥AC,
解:(Ⅰ)证明:∵EA⊥平面ABC,AB⊥AC,
∴直线AB,AC,AE两两垂直,
以A为原点,以AB,AC,AE为坐标轴建立空间直角坐标系A-xyz,设CD=1,则AB=AC=AE=2,
∴A(0,0,0),B(2,0,0),C(0,2,0),D(0,2,1),E(0,0,2),
∵M是BD中点,∴M(1,1,$\frac{1}{2}$),
∴$\overrightarrow{AE}$=(0,0,2),$\overrightarrow{AM}$=(1,1,$\frac{1}{2}$),$\overrightarrow{BC}$=(-2,2,0),
∴$\overrightarrow{AE}•\overrightarrow{BC}$=0,$\overrightarrow{AM}•\overrightarrow{BC}$=0,
∴AE⊥BC,AM⊥BC,
又AM?平面AME,AE?平面AME,AE∩AM=A,
∴BC⊥平面AME.
(II)$\overrightarrow{BD}$=(-2,2,1),$\overrightarrow{AC}$=(0,2,0),$\overrightarrow{AB}$=(2,0,0),
设$\overrightarrow{BM}=λ\overrightarrow{BD}$=(-2λ,2λ,λ)(0<λ<1),则$\overrightarrow{AM}$=$\overrightarrow{AB}+\overrightarrow{BM}$=(2-2λ,2λ,λ),
设平面AMC的法向量为$\overrightarrow{n}$=(x,y,z),
则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{AC}=0}\\{\overrightarrow{n}•\overrightarrow{AM}=0}\end{array}\right.$,∴$\left\{\begin{array}{l}{2y=0}\\{(2-2λ)x+2λy+zλ=0}\end{array}\right.$,令x=1得$\overrightarrow{n}$=(1,0,2-$\frac{2}{λ}$),
∴cos<$\overrightarrow{BD},\overrightarrow{n}$>=$\frac{\overrightarrow{BD}•\overrightarrow{n}}{|\overrightarrow{BD}||\overrightarrow{n}|}$=-$\frac{\frac{2}{λ}}{3×\sqrt{1+(2-\frac{2}{λ})^{2}}}$=-$\frac{2}{3\sqrt{5{λ}^{2}-8λ+4}}$,
令$\frac{2}{3\sqrt{5{λ}^{2}-8λ+4}}$=sin60°=$\frac{\sqrt{3}}{2}$,得5λ2-8λ+$\frac{92}{27}$=0,
△=64-4×5×$\frac{92}{27}$<0,∴方程无解,
∴BD上不存在点M,使得直线BD与平面AMC所成的角为60°.
点评 本题主要考查了用空间向量求直线间的夹角,以及线面平行的判定和线面垂直的判定、异面直线所成角,同时考查了计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 2$\sqrt{5}$ | B. | $\sqrt{5}$ | C. | 3$\sqrt{5}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 对任意的正数M,存在x∈(0,1),使f(x)≥M | |
| B. | 存在正数M,对任意的x∈(0,1),使f(x)≤M | |
| C. | 对任意的x1,x2∈(0,1)且x1<x2,有f(x1)<f(x2) | |
| D. | 对任意的x1,x2∈(0,1)且x1<x2,有f(x1)>f(x2) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 轿车A | 轿车B | 轿车C | |
| 舒适型 | 100 | 150 | z |
| 标准型 | 300 | 450 | 600 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1009 | B. | -2017 | C. | 2017 | D. | -1009 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{6}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{4}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,2] | B. | [2,4) | C. | [2,+∞) | D. | [2,3] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com