练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    14．在等差数列{an}中，前n项和为Sn，且S2011=-2011，a1012=3，则S2017等于（　　）
    A．1009B．-2017C．2017D．-1009

    分析 由等差数列{an}，S2011=-2011，可得S2011=-2011=$\frac{2011×（{a}_{1}+{a}_{2011}）}{2}$=2011a1006，再利用求和公式与性质即可得出．

    解答 解：由等差数列{an}，S2011=-2011，
    ∴S2011=-2011=$\frac{2011×（{a}_{1}+{a}_{2011}）}{2}$=2011a1006，
    ∴a1006=-1，a1012=3，
    则S2017=$\frac{2017（{a}_{1}+{a}_{2017}）}{2}$=$\frac{2017（{a}_{1006}+{a}_{1012}）}{2}$=2017．
    故选：C．

    点评 本题考查了等差数列的通项公式求和公式及其性质，考查了推理能力与计算能力，属于中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    10．函数f（x）=$\left\{\begin{array}{l}{\frac{lnx}{1+x}（x＞0）}\\{\frac{ln（-x）}{1-x}（x＜0）}\end{array}\right.$的图象大致是（　　）
    A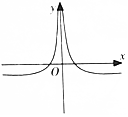．B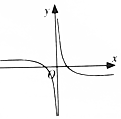．C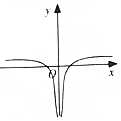．D．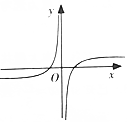

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    5．已知函数f（x）=ex-a+lnx．
    （Ⅰ）若a=1，求证：当x＞1时，f（x）＞2x-1；
    （Ⅱ）若存在x0≥e，使f（x0）＜2lnx0，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    2．如图所示的几何体ABCDE，EA⊥平面ABC，EA∥DC，AB⊥AC，EA=AB=AC=2DC，M是线段BD上的动点．
    （Ⅰ）当M是BD的中点时，求证：BC⊥平面AME；
    （Ⅱ）是否存在点M，使得直线BD与平面AMC所成的角为60°，若存在，确定点M的位置；若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    9．已知f（x）=ax2+（b-a）x+c-b（其中a＞b＞c），若a+b+c=0，x1、x2为f（x）的两个零点，则|x1-x2|的取值范围为（　　）
    A．（$\frac{3}{2}$，2$\sqrt{3}$）B．（2，2$\sqrt{3}$）C．（1，2）D．（1，2$\sqrt{3}$）

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    19．设变量x，y满足约束条件：$\left\{\begin{array}{l}{x-y≤0}\\{x+2y≤3}\\{4x-y≥-6}\end{array}\right.$，则z=|x-2y+1|的取值范围为（　　）
    A．[0，4]B．[0，3]C．[3，4]D．[1，3]

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    6．已知x，y满足：$\left\{{\begin{array}{l}{x≥0}\\{x+y≤2}\\{x-y≤0}\end{array}}\right.$，若目标函数z=ax+y取最大值时的最优解有无数多个，则实数a的值是（　　）
    A．0B．-1C．±1D．1

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    3．已知x，y∈R．
    （Ⅰ）若x，y满足$|{x-3y}|＜\frac{1}{2}$，$|{x+2y}|＜\frac{1}{6}$，求证：$|x|＜\frac{3}{10}$；
    （Ⅱ）求证：x4+16y4≥2x3y+8xy3．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    4．点P（x，y）的坐标满足约束条件$\left\{\begin{array}{l}x-2y≥0\\ x+2y+4≥0\\ 7x+2y-8≤0\end{array}\right.$，由点P向圆C：（x+2）2+（y-1）2=1作切线PA，切点为A，则线段|PA|的最小值为（　　）
    A．$\frac{{4\sqrt{5}}}{5}$B．$\frac{{\sqrt{55}}}{5}$C．$\sqrt{19}$D．$\frac{{\sqrt{33}}}{2}$

    查看答案和解析>>

    同步练习册答案