
已知函数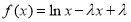 (
(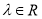 ).
).
(1)求函数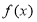 的单调区间;
的单调区间;
(2)请问,是否存在实数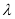 使
使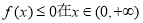 上恒成立?若存在,请求实数
上恒成立?若存在,请求实数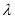 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(1)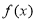 在
在 上单调递增,在
上单调递增,在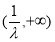 上单调递减;(2)存在,
上单调递减;(2)存在,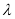 =1。
=1。
【解析】
试题分析:(1)1、求定义域,2、求导数,然后令导数等于0,解出导函数根,再由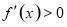 ,得出
,得出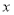 的取值范围,则
的取值范围,则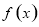 在此区间内单调递增,又由
在此区间内单调递增,又由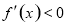 ,得出
,得出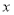 的取值范围,则
的取值范围,则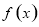 在此区间内单调递减;(2)对于恒成立问题,一般要求出函数在区间内的最大值或最小值。即
在此区间内单调递减;(2)对于恒成立问题,一般要求出函数在区间内的最大值或最小值。即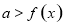 恒成立,则
恒成立,则 ,
,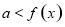 恒成立,则
恒成立,则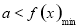 ,本题要讨论
,本题要讨论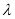 的取值范围,再结合函数的单调性即可求解。
的取值范围,再结合函数的单调性即可求解。
试题解析:(1)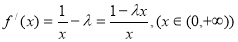 2分
2分
当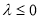 时,
时,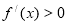 恒成立,
恒成立,
则函数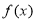 在
在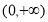 上单调递增 4分
上单调递增 4分
当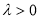 时,由
时,由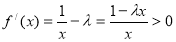 得
得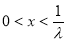
则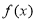 在
在 上单调递增,在
上单调递增,在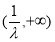 上单调递减 6分
上单调递减 6分
(2)存在. 7分
由(1)得:当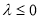 时,函数
时,函数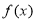 在
在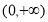 上单调递增
上单调递增
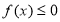 显然不成立;
显然不成立;
当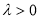 时,
时,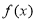 在
在 上单调递增,在
上单调递增,在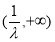 上单调递减
上单调递减
∴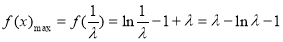 ,
,
只需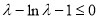 即可 9分
即可 9分
令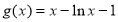
则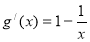 ,
,
函数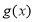 在
在 上单调递减,在
上单调递减,在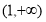 上单调递增.
上单调递增.
∴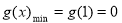 , 10分
, 10分
即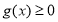 对
对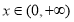 恒成立,
恒成立,
也就是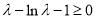 对
对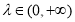 恒成立,
恒成立,
∴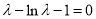 解得
解得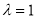 ,
,
∴若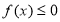 在
在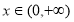 上恒成立,
上恒成立,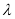 =1. 12分
=1. 12分
考点:1、利用导数研究函数的单调性问题;2、不等式恒成立问题;3、分类讨论思想


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:高中数学 来源:2015届福建省晋江市高二下学期期末理科数学试卷(解析版) 题型:选择题
如图是根据某赛季甲、乙两名篮球运动员每场比赛得分情况画出的茎叶图.从这个茎叶图可以看出甲、乙两名运动员得分的中位数分别是( ).

A.31,26 B.36,23 C.36,26 D.31,23
查看答案和解析>>
科目:高中数学 来源:2015届福建省四地六校高二下学期第一次月考文科数学试卷(解析版) 题型:填空题
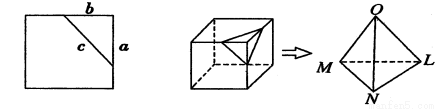
在平面上,我们用一直线去截正方形的一个角,那么截下的一个直角三角形,按如图所标边长,由勾股定理有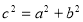 .设想正方形换成正方体,把截线换成如图截面,这时从正方体上截下三条侧棱两两垂直的三棱锥
.设想正方形换成正方体,把截线换成如图截面,这时从正方体上截下三条侧棱两两垂直的三棱锥 ,如果用
,如果用 表示三个侧面面积,
表示三个侧面面积,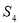 表示截面面积,那么类比得到的结论是 .
表示截面面积,那么类比得到的结论是 .
查看答案和解析>>
科目:高中数学 来源:2015届福建省四地六校高二下学期第一次月考文科数学试卷(解析版) 题型:选择题
观察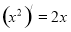 ,
,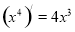 ,
,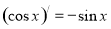 ,由归纳推理可得:若定义在
,由归纳推理可得:若定义在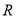 上的函数
上的函数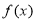 满足
满足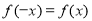 ,记
,记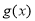 为
为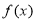 的导函数,则
的导函数,则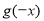 =( )
=( )
A.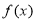 B.
B.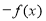 C.
C.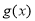 D.
D.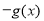
查看答案和解析>>
科目:高中数学 来源:2015届福建省高二下学期期中考试理科数学试卷(解析版) 题型:填空题
已知有限集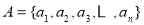
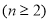 .如果
.如果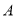 中元素
中元素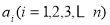 满足
满足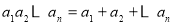 ,就称
,就称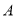 为“复活集”,给出下列结论:
为“复活集”,给出下列结论:
①集合 是“复活集”;
是“复活集”;
②若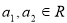 ,且
,且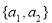 是“复活集”,则
是“复活集”,则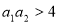 ;
;
③若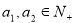 ,则
,则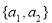 不可能是“复活集”;
不可能是“复活集”;
④若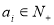 ,则“复合集”
,则“复合集”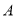 有且只有一个,且
有且只有一个,且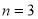 .
.
其中正确的结论是 .(填上你认为所有正确的结论序号).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com